Cuprins
Progresii (aritmetice, geometrice)
Funcții (definiție, injectivitate, surjectivitate, compunerea, inversabilitate)
Principiul inducţiei matematice
Combinatorică (permutări, aranjamente, combinări)
Binomul lui Newton (sume remarcabile)
Funcţii cu domeniul şi codomeniul mulţimi finite
Funcţia de gradul întâi (graficul, monotonia, semnul)
Funcţia de gradul al doilea (forma canonică, ecuația de gr. al II-lea, monotonia, semnul)
Suma și produsul rădăcinilor (Realațiile lui Viète pentru ec. de gr II)
Funcţiile modul şi signum (semnul)
Polinoame și ecuații algebrice
Structuri algebrice (monoizi, grupuri, inele, corpuri, (izo)morfisme)
Formule de calcul prescurtat
$(a+b)^2=a^2+2 a b+b^2$
$(a-b)^2=a^2-2 a b+b^2$
$(a+b+c)^2=a^2+b^2+c^2+2 a b+2 b c+2 c a$
$a^2-b^2=(a-b)(a+b)$
$a^2+b^2 \text { nu se poate descompune in } \mathbb{R}$
$a^2+b^2=(a-i b)(a+i b) \text { in } \mathbb{C}$
$x^2-(a+b) x+a b=(x-a)(x-b)$
$(a+b)^3=a^3+3 a^2 b+3 a b^2+b^3$
$(a-b)^3=a^3-3 a^2 b+3 a b^2-b^3$
$a^3+b^3=(a+b)\left(a^2-a b+b^2\right)$
$a^3-b^3=(a-b)\left(a^2+a b+b^2\right)$
$x^3-(a+b+c) x^2+(a b+b c+c a) x-a b c=(x-a)(x-b)(x-c)$
$a^n-b^n=(a-b) \underbrace{\left(a^{n-1}+a^{n-2} b+a^{n-3} b^2+\cdots+a b^{n-2}+b^{n-1}\right)}_{n \text { termeni }}$
$a^{2 p+1}+b^{2 p+1}=(a+b) \underbrace{\left(a^{2 p}-a^{2 p-1} b+\cdots-a b^{2 p-1}+b^{2 p}\right)}_{2 p+1 \text { termeni }}$
Progresii aritmetice şi progresii geometrice
Progresia aritmetică
$ a_1, a_2, \ldots, a_n, \ldots $
$ a_n=a_1+r \cdot(n-1) \quad(r \neq 0) $
$ r=a_{k+1}-a_k $
$ S_n=a_1+a_2+\ldots+a_n $
$ S_n=\frac{\left(a_n+a_1\right) \cdot n}{2} \quad\left(S_1=a_1\right) $
$ a_k=\frac{a_{k-1}+a_{k+1}}{2}$
Progresia geometrică
$ a_1, a_2, \ldots, a_n, \ldots $
$ a_n=a_1 \cdot q^{n-1} \quad(q \neq 0 ; 1) $
$ q=\frac{a_{k+1}}{a_k} \quad\left(a_k \neq 0\right) $
$ S_n=a_1+a_2+\ldots+a_n $
$ S_n=a_1 \cdot \frac{1-q^n}{1-q} \quad\left(S_1=a_1\right) $
$ a_k=\sqrt{a_{k-1} \cdot a_{k+1}} \quad\left(q>0, \quad a_1>0\right)$
Funcţii
Fie $A$ şi $B$ două mulţimi nevide; se numeşte funcţie definită pe $A$ cu valori în $B$ orice lege de corespondenţă (relaţie) care asociază fiecărui element $x \in A$ un unic element $y \in B$.
Notaţia ” $f: A \rightarrow B, y=f(x)$ ” se citeşte “funcţia $f$ definită pe $A$ cu valori în $B$ de relaţia $y=f(x)$ “.
Mulţimea $A$ este domeniul de definiție al funcţiei $f$ iar mulţimea $B$ reprezintă domeniul de valori al acesteia.
Mulţimea $G_f={(x, f(x)) \mid x \in A}$ poartă numele de grafic al funcţiei.
Funcţii bijective
Funcţia $f: A \rightarrow B$ este injectivă dacă şi numai dacă este îndeplinită următoarea proprietate:
$(\forall) x_1, x_2 \in A \operatorname{din} x_1 \neq x_2$ rezultă $f\left(x_1\right) \neq f\left(x_2\right)$.
În practică, pentru dovedirea injectivităţii, acestă formă a definiţiei poate fi dificil de utilizat. Este preferată formularea (logic echivalentă)
$(\forall) x_1, x_2 \in A \operatorname{din} f\left(x_1\right)=f\left(x_2\right)$ rezultă $x_1=x_2$.
Dacă există cel puţin o pereche de elemente $x_1, x_2$ din domeniul de definiție $A$ cu $x_1 \neq x_2$ dar $f\left(x_1\right)=f\left(x_2\right)$ atunci funcţia $f$ nu este injectivă.
Interpretarea geometrică a injectivităţii pentru funcţii reale ( $B \subset \mathbb{R}$ ) de variabilă reală $(A \subset \mathbb{R})$ este sugestivă:
$f: A \rightarrow B$ este injectivă d.d. orice dreaptă paralelă axei $O x$ prin punctele $y \in B$, intâlneşte graficul funcţiei $f$ in cel mult un punct.
Imaginea funcţiei $f: A \rightarrow B$ este submulţimea domeniului de valori $B$ alcătuită din toate elementele de forma $y=f(x)$ :
$$
\operatorname{Im}(f)={y \in B \mid(\exists) x \in A \text { a.î. } y=f(x)} \text {. }
$$
Funcţia $f: A \rightarrow B$ este surjectivă dacă şi numai dacă $\operatorname{Im}(f)=B$ sau, altfel spus,
$(\forall) y \in B$ ecuaţia $y=f(x)$ are cel puţin o soluţie $x \in A$.
Interpretarea geometrică a surjectivităţii pentru funcţii reale ( $B \subset \mathbb{R}$ ) de variabilă reală $(A \subset \mathbb{R})$:
$f: A \rightarrow B$ este surjectivă d.d. orice dreaptă paralelă axei $O x$ prin punctele $y \in B$, întâlneşte graficul funcţiei $f$ în cel puţin un punct.
Funcţia $f: A \rightarrow B$ este bijectivă dacă şi numai dacă $f$ este şi injectivă şi surjectivă.
Interpretarea geometrică a bijectivităţii pentru funcţii reale ( $B \subset \mathbb{R}$ ) de variabilă reală $(A \subset \mathbb{R})$ :
$f: A \rightarrow B$ este bijectivă d.d. orice dreaptă paralelă axei $O x$ prin punctele $y \in B$, întâlneşte graficul funcţiei $f$ intr-un singur punct.
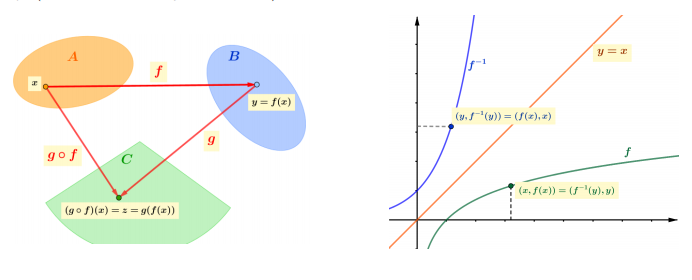
Compunerea funcţiilor
Fie funcţiile $f: A \rightarrow B$ şi $g: B \rightarrow C$ definite prin relaţiile $y=f(x)$, respectiv $z=g(y)$. Funcţia ce asociază fiecărui element $x$ din mulțimea $A$ elementul $z=g(f(x))$ din mulțimea $C$ se numeşte funcţie compusă şi se notează prin $g \circ f$. Mai precis, $g \circ f: A \rightarrow C$ este definită prin
$$
(g \circ f)(x)=g(f(x))
$$
Evident, ordinea în care se efectuează operaţia de compunere nu este aleatoare, ci este bine determinată: domeniul de definiție al funcţiei $g$ (pe prima poziţie în expresia $g \circ f$ ) trebuie să coincidă cu domeniul de valori al funcţiei $f$ (situată pe poziţia secundă).
Funcţii inversabile
Funcţia $f: A \rightarrow B$ este inversabilă dacă şi numai dacă există o funcţie $f^{-1}: B \rightarrow A$ ce verifică relaţiile
$$
\left(f \circ f^{-1}\right)(y)=y \quad(y \in B) \quad \text { şi } \quad\left(f^{-1} \circ f\right)(x)=x \quad(x \in A) .
$$
Funcţia $f^{-1}: B \rightarrow A, x=f^{-1}(y)$ se numeşte inversa funcţiei $f: A \rightarrow B$, $y=f(x)$.
Teoremă
Funcţia $f: A \rightarrow B$ este inversabilă d.d. este bijectivă.
Interpretarea geometrică a inversabilităţii pentru funcţii reale ( $B \subset \mathbb{R}$ ) de variabilă reală $(A \subset \mathbb{R})$ :
$f: A \rightarrow B$ este inversabilă d.d. orice dreaptă paralelă axei $O x$ prin punctele $y \in B$, întâlneşte graficul funcţiei $f$ într-un singur punct.
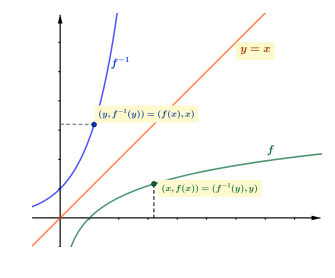
Graficele funcţiei $f$ şi a funcţiei inverse $f^{-1}$, reprezentate in acelaşi sistem de axe, sunt simetrice faţă de prima bisectoare.
Principiul inducţiei matematice
Problemă
Să se arate că propoziţia $\mathbf{P}(n)$ este adevărată pentru orice $n \geq n_0,\left(n_0, n \in \mathbb{N}\right)$.
Etapa I VERIFICAREA Se dovedeşte că $\mathbf{P}\left(n_0\right)$ este adevărată .
Etapa a-II-a PASUL INDUCTIV
Presupunem că $\mathbf{P}(k)$ este adevărată .
Demonstrăm, utilizând presupunerea, că $\mathbf{P}(k+1)$ este adevărată .
În final, $\mathbf{P}\left(n_0\right)$ fiind adevărată (fapt verificat la etapa I ), rezultă că $\mathbf{P}\left(n_0+1\right)$ este de asemenea adevărată (consecinţă a pasului inductiv). Mai departe, conform pasului inductiv, şi propoziţia $\mathbf{P}\left(n_0+2\right)$ este adevărată şi aşa mai departe, $\mathbf{P}(n)$ este adevărată pentru orice $n=n_0+m, m \in \mathbb{N}$.
Sume remarcabile
$1+2+3+\ldots+n =\frac{n \cdot(n+1)}{2}$
$1^2+2^2+3^2+\ldots+n^2 =\frac{n \cdot(n+1) \cdot(2 n+1)}{6}$
$1^3+2^3+3^3+\ldots+n^3 =\left[\frac{n \cdot(n+1)}{2}\right]^2$
Combinatorică
Permutări
$P_n=$ “numărul sistemelor ordonate ce se pot forma cu $\underline{n}$ elemente date”
$P_n=n!=1 \cdot 2 \cdot 3 \cdot \ldots \cdot(n-1) \cdot n$
$n! = (n-1)!\cdot n ; \quad n!=(n-2)!\cdot(n-1) \cdot n$
$(n+1)!= n!\cdot(n+1) ; \quad 0!=1$
Aranjamente
$A_n^m=$”numărul sistemelor ordonate de $ \underline{m}$ elemente ce se pot forma cu $ \underline{n}$ elemente date”.
$A_n^m =n \cdot(n-1) \cdot(n-2) \cdot \ldots \cdot(n-m+1)$
$A_n^m =\frac{n!}{(n-m)!}$
$A_n^0 =1 ; A_n^1=n ; A_n^n=n!$
Combinări
$C_n^m=$ “numărul submulţimilor de $ \underline{m}$ elemente ce se pot forma cu $\underline{n}$ elemente date”.
$C_n^m=\frac{A_n^m}{P_m} ; \quad C_n^m=\frac{n \cdot(n-1) \cdot(n-2) \cdot \ldots \cdot(n-m+1)}{m!}$
$C_n^m=\frac{n!}{m!\cdot(n-m)!}$
$C_n^0=C_n^n=1 ; \quad C_n^1=C_n^{n-1}=n$
$C_n^2=C_n^{n-2}=\frac{n \cdot(n-1)}{2} ; \quad C_n^k=C_n^{n-k}(k \leq n)$
(formula combinărilor complementare)
$C_n^k=\frac{n}{k} \cdot C_{n-1}^{k-1} \quad ; \quad C_n^k=\frac{k+1}{n-k} \cdot C_n^{k+1} ; \quad C_n^k=C_{n-1}^{k-1}+C_{n-1}^k $
Triunghiul lui Pascal (calculul rapid al tuturor combinărilor)
$\begin{array}{llllllllllllll}n=1 & & & & & & 1 \searrow & & \swarrow^1 & & & & && & C_1 \\ n=2 & & & & & 1 \searrow & & \swarrow^2 \searrow & & \swarrow^1 & & & & & & C_2 \\ n=3 & & & & 1 & & 3 & & 3 & & 1 & & & & & C_3 \\ n=4 & & & 1 & & 4 & & 6 & & 4 & & 1 & && & C_4 \\ n=5 & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 && & C_5 \\ n=6 & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1& & \ C_6 & & & & & & & & & \end{array}$
Binomul lui Newton
$(x+y)^n=\sum \limits_{k=0}^n C_n^k \cdot x^{n-k} \cdot y^k$
$(x-y)^n=\sum \limits_{k=0}^n(-1)^k C_n^k \cdot x^{n-k} \cdot y^k$
(suma conţine $n+1$ termeni)
$T_{k+1}=C_n^k \cdot x^{n-k} \cdot y^k$
$T_{k+1}=(-1)^k C_n^k \cdot x^{n-k} \cdot y^k$
(termenul general al dezvoltării, cel de-al $k+1$-termen din dezvoltare)
$\large \frac{T_{k+2}}{T_{k+1}}= \pm \frac{n-k}{k+1} \cdot \frac{y}{x}$
Sume remarcabile
$C_n^0+C_n^1+C_n^2+\ldots+C_n^{n-1}+C_n^n=2^n$
Numărul submulţimilor unei mulţimi finite cu $n$ elemente este $2^n$.
$C_n^0-C_n^1+C_n^2-C_n^3+C_n^4-C_n^5+\ldots=0$
$C_n^0+C_n^2+C_n^4+\ldots=2^{n-1}$
$C_n^1+C_n^3+C_n^5+\ldots=2^{n-1}$
Funcţii cu domeniul şi codomeniul mulţimi finite
Fie $X=${$x_1, x_2, \ldots, x_m$} şi $Y=${$y_1, y_2, \ldots, y_n$} două mulţimi cu $m$ şi respectiv $n$ elemente (distincte), iar $f: X \rightarrow Y$ o funcţie arbitrară.
a) Numărul funcţiilor $f: X \rightarrow Y$ este $n^m$.
b) Dacă $m \leq n$ atunci numărul funcţiilor injective $f: X \rightarrow Y$ este:
$A_n^m=n(n-1) \ldots(n-m+1)$.
Dacă $m>n$ atunci nu pot exista funcţii injective $f: X \rightarrow Y$.
c) Dacă $f: X \rightarrow Y$ este bijectivă atunci $m=n$.
Dacă $m=n$ şi $f: X \rightarrow Y$ este injectivă atunci $f: X \rightarrow Y$ este bijectivă.
Dacă $m=n$ şi $f: X \rightarrow Y$ este surjectivă atunci $f: X \rightarrow Y$ este bijectivă.
d) Numărul funcţiilor bijective $f: X \rightarrow Y$ este $P_n=n!$.
Funcţia de gradul întâi
$f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=a x+b, \quad(a \in \mathbb{R} \backslash{0}, \quad b \in \mathbb{R})$
Graficul funcţiei de gradul întâi este dreapta $y=a x+b$ ce taie axele de coordonate în punctele $\left(-\frac{b}{a}, 0\right)$ şi $(0, b)$.
Soluţia ecuației de gradul întâi $a x+b=0$ este abscisa punctului în care graficul funcţiei intersectează axa $O x: x=-\frac{b}{a}$.
Numărul $a$, coeficientul director al funcţiei de gradul întâi, este panta dreptei $y=a x+b$ şi reprezintă tangenta unghiului $\theta$ pe care dreapta îl face cu semiaxa pozitivă $O x$, măsurat în sens direct trigonometric: $a=\operatorname{tg} \theta$.
Semnul coeficientului director $a$ determină monotonia funcţiei.
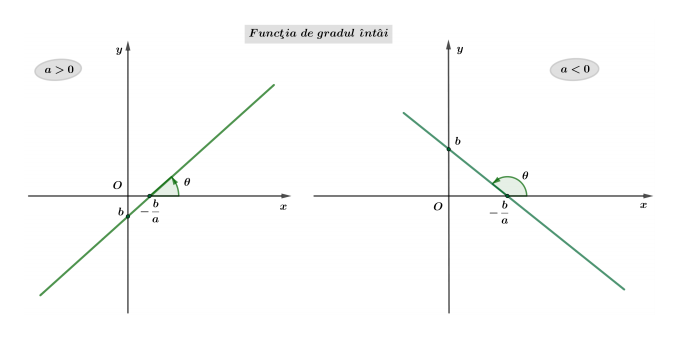
Dacă $a<0$ funcţia este strict descrescătoare: $x_1f\left(x_2\right)$.
Dacă $a>0$ funcţia este strict crescătoare: $x_1<x_2 \Rightarrow f\left(x_1\right)<f\left(x_2\right)$.
Semnul funcţiei de gradul întâi este constant pe intervalele $\left(-\infty,-\frac{b}{a}\right)$ şi $\left(-\frac{b}{a},+\infty\right)$; practic, semnul funcţiei este determinat de semnul coeficientului director $a$.
$
\begin{array}{c|cccc}
x & -\infty & && -\frac{b}{a} & \\
\hline a x+b & & \text { semn contrar lui } a && 0 & & \text { semnul lui } a
\end{array}
$
Funcţia de gradul al doilea
$f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=a x^2+b x+c, \quad(a \in \mathbb{R} \backslash{0}, b, c \in \mathbb{R})$
Forma canonică a expresiei de gradul al doilea se obţine prin izolarea variabilei $x$ într-un pătrat perfect:
$\left.a x^2+b x+c=a\left[\left(x+\frac{b}{2 a}\right)^2-\frac{\Delta}{4 a^2}\right]\right]$ unde $\Delta=b^2-4 a c$
Graficul funcţiei de gradul al doilea este o parabolă având vârful în punctul $V\left(-\frac{b}{2 a},-\frac{\Delta}{4 a}\right)$ şi axa de simetrie $x=-\frac{b}{2 a}$, paralelă cu $O y$. Parabola intersectează axa $O y$ în punctul $(0, c)$.
Dacă $a>0$, vârful $V$ este punct de minim al graficului functiei, iar dacă $a<0$ atunci vârful $V$ este punct de maxim al graficului funcţiei.
Intervalele $\left(-\infty,-\frac{b}{2 a}\right]$ şi $\left[-\frac{b}{2 a},+\infty\right)$ se numesc intervale de monotonie ale funcţiei de gradul doi.
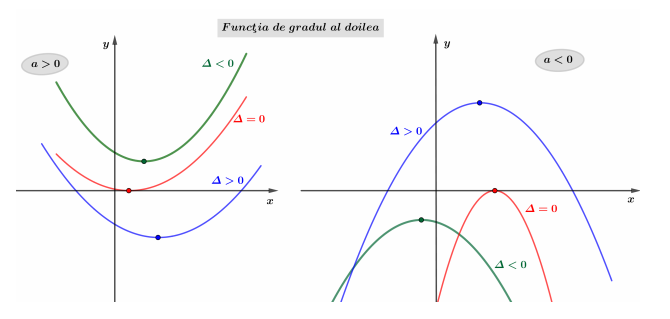
Intersecţia cu axa $O x$ depinde însă de natura rădăcinilor ecuaţiei de gradul al doilea $a x^2+b x+c=0$ :
i) Dacă $\Delta<0$ atunci $a x^2+b x+c$ este o sumă de pătrate şi nu se poate descompune în $\mathbb{R}$; ecuaţia nu are rădăcini reale iar parabola (graficul funcţiei de gradul al doilea) nu întâlneşte axa $O x$.
ii) Dacă $\Delta=0$ atunci $a x^2+b x+c$ se restrânge la un pătrat; ecuaţia are o singură rădăcină reală (dublă) $x=-\frac{b}{2 a}$ iar parabola este tangentă axei $O x$.
iii) Dacă $\Delta>0$ atunci $a x^2+b x+c$ este diferenţă de pătrate şi se descompune ${ }^1$ după cum urmează:
$a x^2+b x+c=a\left(x-x_1\right)\left(x-x_2\right), \quad$ unde $x_{1,2}=\large \frac{-b \pm \sqrt{\Delta}}{2 a}$
În acest caz, ecuaţia are două rădăcini reale distincte $x_1$ şi $x_2$, abscisele punctelor în care parabola întâlneşte axa $O x$.
Obs: Formula de descompunere rămâne valabilă chiar dacă $\Delta<0$; în acest caz $\sqrt{\Delta}=\sqrt{-(-\Delta)}=i \sqrt{-\Delta}$ iar rădăcinile $x_{1,2}=\large \frac{-b \pm i \sqrt{-\Delta}}{2 a}$ sunt numere complexe.
Semnul funcţiei de gradul al doilea este determinat de poziţia graficului (a parabolei) faţă de axa $O x$. Cele şase situaţii descrise mai sus evidenţiază rolul coeficientului director $a$ şi al discriminantului $\Delta$ în studiul semnului. Practic, funcţia de gradul al doilea are semnul coeficientului director $a$ cu o singură excepţie: dacă discriminantul $\Delta$ este strict pozitiv; în acest caz, pe intervalul situat intre rădăcini, funcţia are semn contrar lui $a$.
i) Dacă $\Delta<0$ atunci funcţia de gradul al doilea are acelaşi semn pe întreaga axă reală:
$
\begin{array}{c|ccc}
x & -\infty & & +\infty \\
\hline a x^2+b x+c & & \text { semnul lui } a &
\end{array}
$
ii) Dacă $\Delta=0$ atunci funcţia de gradul al doilea are acelaşi semn pe întreaga axă reală cu excepţia unui singur punct, în care se anulează:
$
\begin{array}{c|ccc}
x & -\infty & -\frac{b}{2 a} & & +\infty \\
\hline a x^2+b x+c & \text { semnul lui } a & 0 & \text { semnul lui } a &
\end{array}
$
iii) Dacă $\Delta>0$ atunci funcţia de gradul al doilea îşi schimbă semnul la trecerea prin rădăcini:
$
\begin{array}{c|ccc}
x & -\infty && & x_1 &&&& x_2 & && +\infty \\
\hline a x^2+b x+c & & \text { semnul lui a }& & 0 & & \text { semn contrar lui a } & & 0 & & \text { semnul lui a } &
\end{array}
$
Relaţiile lui Viète (suma și produsul rădăcinilor) evidenţiază legăturile ce există între coeficienţii şi rădăcinile ecuației, indiferent dacă acestea sunt reale sau complexe:
$S =x_1+x_2=-\large \frac{b}{a}$
$P =x_1 x_2=\large \frac{c}{a}$
Cu ajutorul sumei $S=x_1+x_2$ şi a produsului $P=x_1 x_2$ putem construi întotdeauna ecuaţia de gradul al doilea cu rădăcini date $x_1$ şi $x_2$ :
$x^2-S x+P=0$
Funcţiile modul şi signum (semnul)
$f: \mathbb{R} \rightarrow \mathbb{R}_{+}, \quad f(x)=|x|=\Biggl \{\begin{array}{cc}x & ,\quad x \geq 0 \\ -x & ,\quad x<0\end{array}$
$\text{sgn}: \mathbb{R} \rightarrow \{-1,0,1 \}, \quad \text{sgn}(x)=\Biggl \{\begin{array}{cl}1 & , \quad x>0 \\ 0 & , \quad x=0 \\ -1 & , \quad x<0\end{array}$
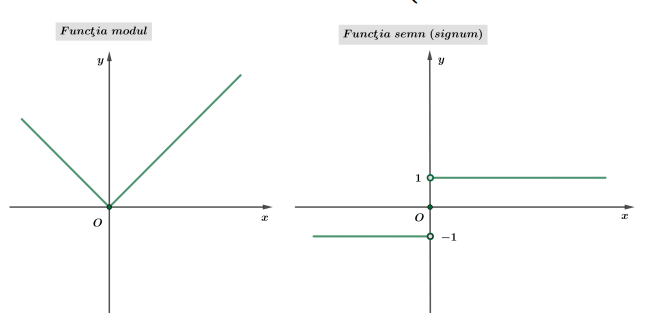
Proprietăţile modulului
i) $\quad|x| \geq 0$ şi $\quad|x|=0 \quad \Leftrightarrow x=0 \quad$ (modulul este pozitiv definit)
ii) $\quad \frac{|x|}{x}=\operatorname{sgn}(x) \quad(x \neq 0)$
iii) $\begin{array}{ll}|\alpha \cdot x|=\alpha \cdot|x| & (\alpha \geq 0) \quad \text { (modulul este multiplicativ) }\end{array}$
iv) $|x+y| \leq|x|+|y| \quad$ (inegalitatea triunghiului)
v) $|x \pm y| \geq||x|-|y||$
Funcţia modul este continuă în origine fără a fi insă derivabilă în acest punct:
$f_s^{\prime}(0)=-1, \quad f_d^{\prime}(0)=1$
Funcţia semn este discontinuă în origine; $x=0$ este punct de discontinuitate de speţa întâi:
$f(0-0)=-1, \quad f(0)=0, \quad f(0+0)=1$
Funcţia parte întreagă
$f: \mathbb{R} \rightarrow \mathbb{Z}, \quad f(x)=[x]$
Proprietăţile părţii întregi
i) $\quad x-1<[x] \leq x<[x]+1$
ii) $[x+n]=n+[x] \quad(n \in \mathbb{Z})$
Funcţia parte întreagă este discontinuă în fiecare punct de abscisă întreagă:
$f(n-0)=n-1 \text { şi } f(n)=f(n+0)=n$
Punctele de abscisă întregă sunt discontinuităţi de speţa întâi.
Funcţia parte întreagă este continuă la dreapta în fiecare punct de abscisă întreagă.
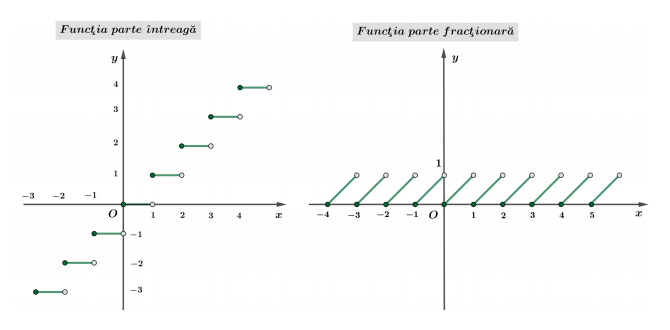
Funcţia parte fracţionară
$f: \mathbb{R} \rightarrow[0,1), \quad f(x)={x}$
${x}=x-[x]$ este partea fracţionară a lui $x$
Funcţia parte fracţionară este periodică cu perioada principală $T=1$ :
$f(x+k)=f(x) \quad(\forall) x \in \mathbb{R}, \quad(\forall) k \in \mathbb{Z}$
Funcţia parte fracţionară este discontinuă în fiecare punct de abscisă întreagă:
$f(n-0)=1 \text { şi } f(n)=f(n+0)=0$
Puteri şi radicali
$f_k: \mathbb{R} \rightarrow \mathbb{R}, \quad f_k(x)=x^k \quad\left(k \in \mathbb{N}^*\right)$
$f:[0,+\infty) \rightarrow[0,+\infty), \quad f(x)=\sqrt[2 n]{x} \quad\left(n \in \mathbb{N}^*\right)$
Rădăcina de ordinul $k=2 n$ a numărului pozitiv a este unica soluţie pozitivă a ecuaţiei $z^{2 n}=a$ şi se notează prin $\sqrt[2 n]{a}$.
Conform acestei definiţii, pentru numerele pozitive $a$ şi $z$, are loc echivalenţa
$\sqrt[2 n]{a}=z \quad \Longleftrightarrow \quad z^{2 n}=a$
Convenim să notăm rădăcina pătrată (rădăcina de ordinul al doilea) simplu prin $\sqrt{ }$ în loc de $\sqrt[2]{ }$.
Observatie
Rădăcina de ordinul doi a numărului 4 este 2 deoarece doar una din rădăcinile ecuaţiei
$z^2=4 \quad \Longleftrightarrow \quad z_{1,2}= \pm 2$
este pozitivă; prin urmare $\sqrt{4}=+2$. Exprimarea $\sqrt{4}= \pm 2$ este greşită în contextul extragerii rădăcinii reale.
$f: \mathbb{R} \rightarrow \mathbb{R}, \quad f(x)=\sqrt[2 n+1]{x} \quad\left(n \in \mathbb{N}^*\right)$
Rădăcina de ordinul $k=2 n+1$ a numărului real a este unica soluţie reală a ecuaţiei $z^k=a$ şi se notează prin $\sqrt[2 n+1]{a}$ :
$\sqrt[2 n+1]{a}=z \quad \Longleftrightarrow \quad z^{2 n+1}=a$
Definiția rădăcinii de ordinul $k$ poate fi extinsă şi în cazul numerelor negative dacă indicele $k$ este impar, $k=2 n+1 \quad\left(n \in \mathbb{N}^*\right)$.
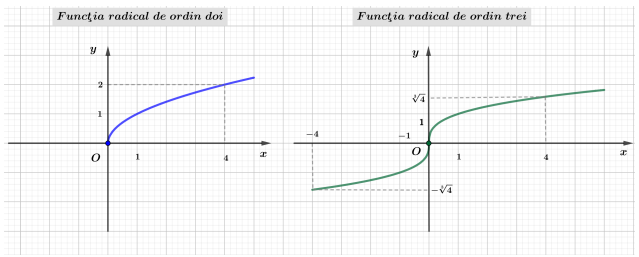
Dreapta $x=0$ (axa $O y$ ) este tangentă vericală la graficul funcţiei radical. Originea $O(0,0)$ este punct de inflexiune cu tangenta verticală la graficul funcţiei radical de ordin impar.
Proprietăţile puterilor şi radicalilor
$a^n=\underbrace{a \cdot a \cdot \ldots \cdot a}_{d e ” n ” \text { ori }} \quad\left(n \in \mathbb{N}^*, \quad a \in \mathbb{R}\right)$
$a^0=1 \quad\left(a \in \mathbb{R}^*\right)$
$a^{-k}=\frac{1}{a^k} \quad\left(k \in \mathbb{Z}, \quad a \in \mathbb{R}^*\right)$
$a^{\frac{p}{q}}=\sqrt[q]{a^p} \quad\left(p \in \mathbb{Z}^, \quad q \in \mathbb{N}^ \backslash{1}, \quad a \in \mathbb{R}_{+}^*\right)$
$\sqrt[n]{a \cdot b}=\sqrt[n]{a} \cdot \sqrt[n]{b} \quad, \quad \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}} \quad(b \neq 0)$
$\sqrt[n \cdot m]{a^{k \cdot m}}=\sqrt[n]{a^k} \quad, \quad \sqrt[n]{a^{n \cdot m}}=a^m$,
$\sqrt[n]{a^m}=(\sqrt[n]{a})^m \quad, \quad \sqrt[n]{\sqrt[m]{a}}=\sqrt[n \cdot m]{a}$.
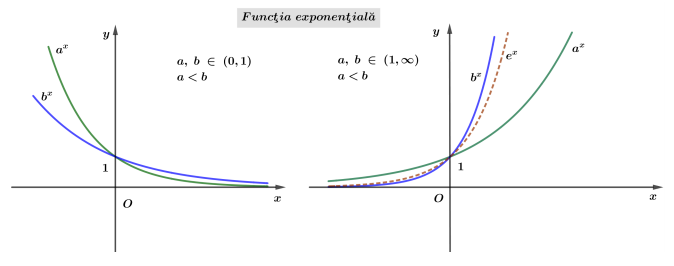
Funcţia exponenţială
$f: \mathbb{R} \rightarrow(0, \infty), f(x)=a^x \quad\left(a \in \mathbb{R}_{+}^* \backslash{1}=(0,1) \cup(1, \infty)\right)$
Funcţia exponenţială cu baza supraunitară este strict crescătoare:
$a \in(1, \infty) \quad x_1<x_2 \quad \Rightarrow \quad a^{x_1}<a^{x_2}$
În plus, au loc relaţiile:
$\begin{array}{ll}
x \lt 0 & 1 \lt a \lt b \Rightarrow a^x \gt b^x \\
x \gt 0 & 1 \lt a \lt b \Rightarrow a^x \lt b^x .
\end{array}$
Funcţia exponenţială cu baza subunitară este strict descrescătoare:
$a \in(0,1) \quad x_1 \lt x_2 \Rightarrow a^{x_1} \gt a^{x_2}.$
În plus, au loc relaţiile:
$\begin{array}{ll}
x \lt 0 & 0 \lt a \lt b \lt 1 \Rightarrow a^x \gt b^x \\
x \gt 0 & 0 \lt a \lt b \lt 1 \Rightarrow a^x \lt b^x
\end{array}$
Proprietăţile funcţiei exponenţiale
i) Proprietăţi de calcul
$a^x \cdot a^y=a^{x+y}; \quad \frac{a^x}{a^y}=a^{x-y}$
$(a \cdot b)^x=a^x \cdot b^x; \quad\left(\frac{a}{b}\right)^x=\frac{a^x}{b^x}$
$\left(a^x\right)^y=a^{x \cdot y}; \quad a^{-x}=\frac{1}{a^x}$
ii) Funcţia exponenţială este bijectivă deoarece este injectivă
$x_1 \neq x_2 \quad \Rightarrow \quad a^{x_1} \neq a^{x_2} \quad\left(\right.$ echivalent $\left.a^{x_1}=a^{x_2} \quad \Rightarrow \quad x_1=x_2\right)$
şi surjectivă
$(\forall) y \in(0,+\infty), \quad (\exists) x \in \mathbb{R}$ a.î. $y=a^x$.
Prin urmare funcţia exponenţială este inversabilă iar inversa ei este funcţia logaritmică cu aceeaşi bază (vezi paragraful ce urmează).
iii) Dreapta $y=0$ (axa $O x$ ) este asimptotă orizontală la graficul funcţiei exponenţiale. În cazul funcţiei exponenţiale cu baza $e=2,718281 \ldots$, limitele la extremităţi sunt
$\lim \limits_{x \rightarrow-\infty} e^x=0 \quad \text { şi } \quad \lim \limits_ {x \rightarrow \infty} e^x=+\infty .$
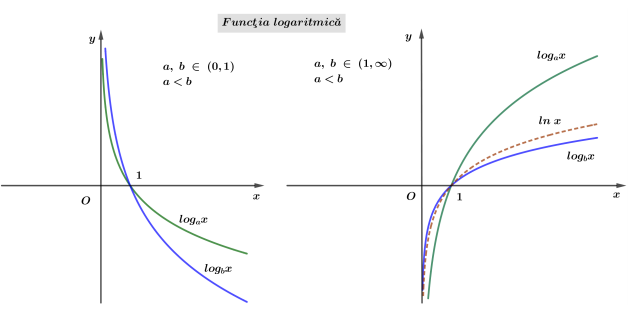
Funcţia logaritmică
$f:(0, \infty) \rightarrow \mathbb{R}, f(x)=\log_a x \quad\left(a \in \mathbb{R}{+}^* \backslash{1}=(0,1) \cup(1, \infty)\right)$
Logaritmul unui număr pozitiv $x$ calculat in baza a $\left(a \in \mathbb{R}_{+}^* \backslash{1}\right)$ se notează $\log _a x$ şi reprezintă puterea la care trebuie ridicată baza $a$ pentru a obţine $x$.
Conform acestei definiţii, pentru numerele strict pozitive $x$ şi $a, a \neq 1$, are loc echivalenţa
$\log _a x=y \quad \Longleftrightarrow \quad a^y=x$
Logaritmii cel mai des întâlniţi în practică sunt logaritmul zecimal $\left(\log _{10}\right)$ pentru calcule numerice şi logaritmul natural $\left(\log _e\right)$, cu baza $e=2,718281 \ldots$, la capitolul de Analiză matematică. Pentru simplitatea scrierii se utilizează notaţiile
$\log _{10} x=\lg x \quad \text { şi } \quad \log _e x=\ln x$
Funcţia logaritmică cu baza supraunitară este strict crescătoare:
$a \in(1, \infty) \quad x_1 \lt x_2 \quad \Rightarrow \quad \log _a x_1 \lt \log _a x_2$
În plus, au loc relaţiile:
$0 \lt x \lt 1, \quad 1 \lt a \lt b \Rightarrow \log _a x \lt \log _b x$
$x \gt 1, \quad 1 \lt a \lt b \Rightarrow \log _a x \gt \log _b x$.
Funcţia logaritmică cu baza subunitară este strict descrescătoare:
$a \in(0,1), \quad x_1\log _a x_2$
În plus, au loc relaţiile:
$0 \lt x \lt 1, \quad 0 \lt a \lt b \lt 1 \Rightarrow \log _a x \lt \log _b x$
$x \gt 1, \quad 0 \lt a \lt b \lt 1 \Rightarrow \log _a x \gt \log _b x$
Proprietăţile funcţiei logaritmice
i) Proprietăţi de calcul
$\log _a x y=\log _a x+\log _a y ; \quad \log _a \frac{x}{y}=\log _a x-\log _a y$
$\log _a 1=0; \quad \log _a a=1$
$\log a x^r=r \log _a x; \quad \log {a^r} x=\frac{1}{r} \log _a x$
$\log _a \sqrt[n]{x}=\frac{1}{n} \log _a x; \quad \log _a \frac{1}{x}=-\log _a x$
ii) Funcţia logaritmică este bijectivă deoarece este injectivă
$x_1 \neq x_2 \Rightarrow \log _a x_1 \neq \log _a x_2 \quad\left(\right.$ echivalent $\left.\log _a x_1=\log _a x_2 \Rightarrow x_1=x_2\right)$
şi surjectivă
$(\forall) y \in \mathbb{R}, \quad ( \exists) x \in(0,+\infty)$ a.î. $y=\log _a x$.
Prin urmare funcţia logaritmică este inversabilă iar inversa ei este funcţia exponenţială cu aceeaşi bază.
$a^{\log _a x}=x, \quad(\forall) x \in(0,+\infty)$
$\log _a a^y=y, \quad(\forall) y \in \mathbb{R}$
În figura de mai jos, funcţiile exponenţială cu baza $e$ şi inversa ei, logaritmul natural, sunt reprezentate în acelaşi sistem de coordonate. Graficele celor două funcţii sunt simetrice faţă de prima bisectoare.
iii) Dreapta $x=0$ (axa $O y$ ) este asimptotă verticală la graficul funcţiei logaritmice. În cazul logaritmului natural, limitele la extremităţi sunt
$\lim\limits_ {\substack{x \rightarrow 0 \\ x>0}} \ln x=-\infty \quad$ şi $\quad \lim\limits_ {x \rightarrow \infty} \ln x=+\infty$.
iv) Formulele de schimbare a bazei logaritmilor
$\log _a A=\log _b A \cdot \log _a b; \quad \log _a A=\large \frac{\log _b A}{\log _b a}$
$\log _a b= \large \frac{1}{\log _b a}$
Polinoame și ecuații algebrice
Împărţirea polinoamelor. Divizibilitate.
$f, g \in \mathbb{C}[X]$ polinoame având gradele $n=\text{grad}(f)$ şi respectiv $m=\text{grad}(g)$
$n \geq m \Rightarrow f: g=c$ rest $r, \quad$ unde $ \text{grad}(r)<m, \quad \text{grad}(c)=n-m$
Teorema împărţirii cu rest
$f: g=c$ rest $r \quad$ d.d. $\quad f=g \cdot c+r \quad$ (proba împărţirii)
Polinomul $f$ este divizibil prin $g$ dacă şi numai dacă $r \equiv 0$ (citeşte: $r$ este polinomul identic nul sau, mai precis, coeficienţii restului $r$ sunt toţi nuli).
Polinoamele $f$ şi $g$ sunt prime intre ele dacă cel mai mare divizor comun al lor este 1 (se notează: $(f, g)=1$ ).
Teorema lui Bézout
Restul împărţirii lui $f$ prin $(x-a)$ este $r=f(a)$.
Consecinţe:
a) $f$ este divizibil prin $(x-a) \Leftrightarrow f(a)=0$
b) $f$ este divizibil prin $g \Leftrightarrow$ toate rădăcinile lui $g$ sunt rădăcini (cu multiplicităţi identice) pentru $f$.
Teorema fundamentală a algebrei
Orice polinom cu coeficienţi complecşi are cel puţin o rădăcină complexă.
Consecinţă
Orice polinom $f=a_0 X^n+a_1 X^{n-1}+\cdots+a_{n-1} X+a_n \in \mathbb{C}[X]$ are exact $n$ rădăcini complexe $x_1, x_2, \ldots, x_n$ (distincte sau nu) şi prin urmare se descompune în factori primi de gradul întâi:
$f=a_0\left(X-x_1\right)^{n_1} \cdot\left(X-x_2\right)^{n_2} \cdot \ldots \cdot\left(X-x_k\right)^{n_k}$
unde $n_1, n_2, \ldots, n_k$ reprezintă multiplicităţile rădăcinilor distincte $x_1, x_2, \ldots, x_k$.
Relaţiile lui Viète
$\text{gr}(f)=2 \Rightarrow f=a_0 X^2+a_1 X+a_2$
$f=a_0\left(X-x_1\right)\left(X-x_2\right)=a_0 X^2-a_0\left(x_1+x_2\right) X+a_0 x_1 x_2$
$\Rightarrow \Biggl \{\begin{array}{l}x_1+x_2=-\large \frac{a_1}{a_0} \\ x_1 x_2=\large \frac{a_2}{a_0}\end{array}$
$\text{gr}(f)=3 \Rightarrow f=a_0 X^3+a_1 X^2+a_2 X+a_3$
$f=a_0\left(X-x_1\right)\left(X-x_2\right)\left(X-x_3\right)=$
$=a_0 X^3-a_0\left(x_1+x_2+x_3\right) X^2+a_0\left(x_1 x_2+x_2 x_3+x_3 x_1\right) X-a_0 x_1 x_2 x_3$
$\Rightarrow \begin{cases}x_1+x_2+x_3 & =-\frac{a_1}{a_0} \\ x_1 x_2+x_2 x_3+x_3 x_1 & =\frac{a_2}{a_0} \\ x_1 x_2 x_3 & =-\frac{a_3}{a_0}\end{cases}$
$\text{gr}(f)=4 \Rightarrow f=a_0 X^4+a_1 X^3+a_2 X^2+a_3 X+a_4$
$f=a_0\left(X-x_1\right)\left(X-x_2\right)\left(X-x_3\right)\left(X-x_4\right)=$
$=a_0 X^4-a_0\left(x_1+x_2+x_3+x_4\right) X^3+a_0\left(x_1 x_2+x_2 x_3+\cdots\right.$
$\Rightarrow \begin{cases}x_1+x_2+x_3+x_4 & =-\frac{a_1}{a_0} \\ x_1 x_2+x_2 x_3+x_3 x_4+x_4 x_1+x_2 x_4+x_1 x_3 & =\frac{a_2}{a_0}\quad \quad \heartsuit \\ x_1 x_2 x_3+x_2 x_3 x_4+x_3 x_4 x_1+x_4 x_1 x_2 & =-\frac{a_3}{a_0} \quad \diamondsuit \\ x_1 x_2 x_3 x_4 & =\frac{a_4}{a_0}\end{cases}$
$\heartsuit $ se scrie mai convenabil: $\quad x_1 x_2+x_3 x_4+\left(x_1+x_2\right)\left(x_3+x_4\right)=\frac{a_2}{a_0}$
$\diamondsuit $ se scrie mai convenabil: $\quad x_1 x_2\left(x_3+x_4\right)+x_3 x_4\left(x_1+x_2\right)=-\frac{a_3}{a_0}$
Tipuri speciale de ecuaţii de grad superior
a) Ecuaţii binome
$x^n-a=0$
- se scrie $a$ sub formă trigonometrică: $\quad a=r(\cos t+i \sin t)$
- se extrage rădăcina complexă de ordinul $n$ :
$x_k \in\left\lbrace\left.\sqrt[n]{r}\left(\cos \frac{t+2 k \pi}{n}+i \sin \frac{t+2 k \pi}{n}\right) \right\rvert\, k \in{0,1,2, \ldots,(n-1)}\right\rbrace$
b) Ecuaţii bipătrate şi tripătrate
$x^4+a x^2+b=0 \quad$ substituţia $\quad x^2=y$
$x^6+a x^3+b=0 \quad$ substituţia $\quad x^3=y$
c) Ecuaţii reciproce
- Ecuaţia reciprocă de gradul 3
$a x^3+b x^2+b x+a=0$
admite rădăcina $x_1=-1$.
Se aplică schema lui Horner şi se obţine o ecuaţie de gradul doi.
- Ecuaţia reciprocă de gradul 4
$a x^4+b x^3+c x^2+b x+a=0$
Prin împărţirea cu $x^2$ rezultă $a x^2+b x+c+\frac{b}{x}+\frac{a}{x^2}=0$, echivalent, după gruparea termenilor
$a\left(x^2+\frac{1}{x^2}\right)+b\left(x+\frac{1}{x}\right)+c=0$.
Se face substituţia $t=x+\frac{1}{x} \Rightarrow t^2-2=x^2+\frac{1}{x^2}$.
Se rezolvă ecuaţia redusă: $a\left(t^2-2\right)+b t+c=0$.
Se revine la variabila $x$ rezolvând ecuaţiile de gradul al doilea: $x+\frac{1}{x}=t_1$ şi $x+\frac{1}{x}=t_2$.
- Ecuaţia reciprocă de gradul 5
admite rădăcina $x=-1$.
Se aplică schema lui Horner şi se obţine o ecuaţie reciprocă de gradul 4:
$\begin{array}{c|cccccc} & a & b & c & c & b & a \\ \hline-1 & a & b-a & -b+a+c & b-a & a & 0 \end{array}$
$a x^4+(b-a) x^3+(a-b+c) x^2+(b-a) x+a=0$
d) Ecuaţii cu coeficienţi întregi
$f=0, \quad f \in \mathbb{Z}[X]$
$a_0 x^n+a_1 x^{n-1}+\ldots+a_n=0$
Rădăcinile întregi se află printre divizorii termenului liber $a_n$
Rădăcinile raţionale $\frac{p}{q}$ se află printre fracţiile $\frac{p}{q}$ cu
$p$, divizor al termenului liber $a_n$
$q$, divizor al coeficientului director $a_0$
e) Ecuaţii cu coeficienţi raţionali
$f=0, \quad f \in \mathbb{Q}[X]$
$a+b \sqrt{q}, \quad (a, b \in \mathbb{Q}, b \neq 0, q$ nu este pătrat perfect$)$
Dacă $x_1=a+b \sqrt{q}$ este rădăcină pentru $f$ atunci $x_2=a-b \sqrt{q}$ este de asemenea rădăcină pentru $f$, caz în care $f$ este divizibil prin
$(X-a-b \sqrt{q})(X-a+b \sqrt{q})=(X-a)^2-b^2 q.$
f) Ecuaţii cu coeficienţi reali
$f=0, \quad f \in \mathbb{R}[X]$
$a+i b, \quad(a, b \in \mathbb{R}, b \neq 0)$
Dacă $x_1=a+i b$ este rădăcină pentru $f$ atunci $x_2=a-i b$ este de asemenea rădăcină pentru $f$, caz în care $f$ este divizibil prin
$(X-a-i b)(X-a+i b)=(X-a)^2+b^2$.
Matrici şi determinanţi
$A=\left(\begin{array}{ccccccc}a_{11} & \ldots & a_{1 j-1} & a_{1 j} & a_{1 j+1} & \ldots & a_{1 n} \\ \vdots & & \vdots & \vdots & \vdots & & \vdots \\ a_{i-11} & \ldots & a_{i-1 j-1} & a_{i-1 j} & a_{i-1 j+1} & \ldots & a_{i-1 n} \\ a_{i 1} & \ldots & a_{i j-1} & a_{i j} & a_{i j+1} & \ldots & a_{i n} \\ a_{i+11} & \ldots & a_{i+1 j-1} & a_{i j} & a_{i+1 j+1} & \ldots & a_{i+1 n} \\ \vdots & & \vdots & \vdots & \vdots & & \vdots \\ a_{m 1} & \ldots & a_{m j-1} & a_{m j} & a_{m j+1} & \ldots & a_{m n}\end{array}\right)=\left(a_{i j}\right)_{\substack{1 \leq i \leq m \\ 1 \leq j \leq n}}$
sau
$A=\left[\begin{array}{ccccccc}a_{11} & \ldots & a_{1 j-1} & a_{1 j} & a_{1 j+1} & \ldots & a_{1 n} \\ \vdots & & \vdots & \vdots & \vdots & & \vdots \\ a_{i-11} & \ldots & a_{i-1 j-1} & a_{i-1 j} & a_{i-1 j+1} & \ldots & a_{i-1 n} \\ a_{i 1} & \ldots & a_{i j-1} & a_{i j} & a_{i j+1} & \ldots & a_{i n} \\ a_{i+11} & \ldots & a_{i+1 j-1} & a_{i j} & a_{i+1 j+1} & \ldots & a_{i+1 n} \\ \vdots & & \vdots & \vdots & \vdots & & \vdots \\ a_{m 1} & \ldots & a_{m j-1} & a_{m j} & a_{m j+1} & \ldots & a_{m n}\end{array}\right]=\left[a_{i j}\right]_{\substack{1 \leq i \leq m \\ 1 \leq j \leq n}}$
Matricea $A$ este o matrice dreptunghiulară de tipul $m \times n$ deoarece are $m$ linii şi $n$ coloane. Dacă numărul de linii coincide cu numărul de coloane $(m=n)$, spunem că $A$ este o matrice pătrată de ordinul $n$.
Operaţii cu matrici
- adunarea matricilor de acelaşi tip: $\left[a_{i j}\right]+\left[b_{i j}\right]=\left[a_{i j}+b_{i j}\right]$;
- inmulţirea cu un scalar $\alpha \in \mathbb{R}$ (sau $\mathbb{C}$ ): $\alpha \cdot\left[a_{i j}\right]=\left[\alpha a_{i j}\right]$;
- inmulţirea matricilor se realizează după regula “linie pe coloană” şi este posibilă doar dacă numărul coloanelor primului termen $\left[a_{i k}\right] \in \mathcal{M}{m \times p}(\mathbb{R})$ este egal cu numărul liniilor celui de-al doilea termen $\left[b{k j}\right] \in \mathcal{M}_{p \times n}(\mathbb{R})$ :
$\left[a_{i k}\right] \cdot\left[b_{k j}\right]=\left[\sum \limits_{k=1}^p a_{i k} b_{k j}\right]$
Spre exemplu, produsul matricii $A$ având trei linii şi două coloane ( $m=3, p=2$ ) cu matricea $B$ formată din două linii şi patru coloane ( $p=2, n=4$ ) este matricea $C=A \cdot B$ cu trei linii şi patru coloane ( $m=3, n=4$ ):
$C=A \cdot B=\left[\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32}\end{array}\right]\left[\begin{array}{llll}b_{11} & b_{12} & b_{13} & b_{14} \\ b_{21} & b_{22} & b_{23} & b_{24}\end{array}\right]=$
$=\left[\begin{array}{llll}a_{11} b_{11}+a_{12} b_{21} & a_{11} b_{12}+a_{12} b_{22} & a_{11} b_{13}+a_{12} b_{23} & a_{11} b_{14}+a_{12} b_{24} \\ a_{21} b_{11}+a_{22} b_{21} & a_{21} b_{12}+a_{22} b_{22} & a_{21} b_{13}+a_{22} b_{23} & a_{21} b_{14}+a_{22} b_{24} \\ a_{31} b_{11}+a_{32} b_{21} & a_{31} b_{12}+a_{32} b_{22} & a_{31} b_{13}+a_{32} b_{23} & a_{31} b_{14}+a_{32} b_{24}\end{array}\right]$.
Chiar dacă se poate calcula $A \cdot B$, în general $B \cdot A$ nu are sens. Mai mult, în cazul matricilor pătrate, deşi produsele $A \cdot B$ şi $B \cdot A$ au ambele sens, în general $A \cdot B \neq B \cdot A$. Cu alte cuvinte, produsul matricelor pătrate nu este o operație comutativă.
Matricea nulă $\mathbf{0}$, matricea cu toate elementele egale cu 0 , este element neutru la adunare.
Matricea pătrată de ordinul $n$, notată $I_n$ şi numită matricea unitate de ordinul $n$, având toate elementele nule cu excepţia celor situate pe diagonala principală, care sunt egale cu 1, este element neutru la înmulţirea matricilor.
Determinantul unei matrici pătrate este numărul (real sau complex) calculat după regula:
$\text{det} A=\sum \limits_{\sigma \in P_n}(-1)^{\text{sgn}(\sigma)} a_{1 \sigma(1)} \cdot a_{2 \sigma(2)} \cdots \cdots a_{n \sigma(n)}$
unde $\sigma$ parcurge toate permutările mulţimii ${1,2,3, \ldots, n}$ iar $\operatorname{sgn}(\sigma)$ desemnează signatura permutării $\sigma$ (adică numărul inversiunilor din $\sigma$ ). Reamintim că numărul de permutări al unei mulţimi cu $n$ elemente este egal cu $n!$, deci suma din definiție are $n!$ termeni.
Calculul unui determinant cu formula din definiţie este laborioasă, nepractică.
Determinantul matricelor de ordinul 2
$\text{det}\left[\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right] \stackrel{\text { not }}{=}\left|\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right|=a_{11} a_{22}-a_{12} a_{21}$
Determinantul matricelor de ordinul 3
$\text{det}\left[\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right] \stackrel{\text { not }}{=}\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|=$
$=a_{11} a_{22} a_{33}+a_{13} a_{21} a_{32}+a_{12} a_{23} a_{31}-\left(a_{13} a_{22} a_{31}+a_{11} a_{23} a_{32}+a_{12} a_{21} a_{33}\right)$
În aplicaţii, pentru calculul determinantului de ordinul al treilea se utilizează regula triunghiurilor sau regula lui Sarrus, reguli ilustrate în figura ce urmează.

Se numeşte complement algebric al elementului $a_{i j}$ din matricea $A$, numărul
$\Gamma_{i j}=(-1)^{i+j}\left|\begin{array}{cccc}a_{11} & a_{1 j-1} & a_{1 j+1} & a_{1 n} \\ a_{i-11} & a_{i-1 j-1} & a_{i-1 j+1} & a_{i-1 n} \\ a_{i+11} & a_{i+1 j-1} & a_{i+1 j+1} & a_{i+1 n} \\ a_{n 1} & a_{n j-1} & a_{n j+1} & a_{n n}\end{array}\right|$
(ce rezultă multiplicând $(-1)^{i+j}$ cu minorul corespunzător elementului $a_{i j}$, adică determinantul matricii obţinute prin eliminarea liniei $i$ şi coloanei $j$ din $A).$
Dezvoltarea determinantului după linia $i$ :
$\text{det} A=a_{i 1} \Gamma_{i 1}+a_{i 2} \Gamma_{i 2}+\cdots+a_{i n} \Gamma_{i n}$
Dezvoltarea determinantului după coloana $j$ :
$\text{det} A=a_{1 j} \Gamma_{1 j}+a_{2 j} \Gamma_{2 j}+\cdots+a_{n j} \Gamma_{n j}.$
Proprietăţile determinanţilor
- Dacă într-o matrice $A$
-toate elementele unei linii (coloane) sunt nule, sau
-două linii (coloane) sunt egale, sau
-două linii (coloane) sunt proporţionale
atunci $\text{det} A=0$. - Dacă la o linie (coloană) a unui determinant se adună elementele corespunzătoare ale altei linii (coloane) multiplicate cu un scalar, valoarea determinantului rămâne neschimbată.
Spre exemplu, în determinantul de ordinul trei ce urmează, la linia întâi este adunată linia a treia multiplicată cu $\alpha :$
$\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|=\left|\begin{array}{ccc}a_{11}+\alpha a_{31} & a_{12}+\alpha a_{32} & a_{13}+\alpha a_{33} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|$ - Dacă se înmulţesc elementele unei linii (sau coloane) din matricea $A$ cu un scalar $\alpha$ atunci determinantul noii matrici este $\alpha \operatorname{det} A$.
- Determinantul produsului dintre un scalar $\alpha$ şi o matrice $A$ de ordinul $n: \text{det}(\alpha A)=\alpha^n \text{det}(A)$.
- Determinantul produsului a două matrici este egal cu produsul determinaţilor acestora: $\operatorname{det}(A \cdot B)=\operatorname{det} A \cdot \operatorname{det} B$.
- O matrice de ordinul $n$ se numeşte matrice triunghiulară dacă toate elementele situate dedesubtul (sau deasupra) unei diagonale sunt nule. Determinantul unei matrici triunghiulare este egal cu produsul elementelor de pe diagonala principală sau $(-1)^n$ multiplicat cu produsul elementelor de pe diagonala secundară, după caz.
- Descompunerea determinantului relativ la o linie (coloană) o ilustrăm în cazul particular al determinantului de ordinul trei, relativ la linia întâi:
$\left|\begin{array}{ccc}a_{11}^{\prime}+a_{11}^{\prime \prime} & a_{12}^{\prime}+a_{12}^{\prime \prime} & a_{13}^{\prime}+a_{13}^{\prime \prime} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|=\left|\begin{array}{ccc}a_{11}^{\prime} & a_{12}^{\prime} & a_{13}^{\prime} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|+\left|\begin{array}{ccc}a_{11}^{\prime \prime} & a_{12}^{\prime \prime} & a_{13}^{\prime \prime} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right|$.
(Trebuie subliniat că această proprietate este valabilă în cazul determinanţilor de orice ordin, indiferent de linia (sau coloana) luată în considerare.) - Matricile pătrate de ordinul al doilea $A=\left[\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right]$ verifică următoarea identitate remarcabilă (Cayley-Hamilton):
$A^2-\left(a_{11}+a_{22}\right) A+\left(a_{11} a_{22}-a_{12} a_{21}\right) I_2=\mathbf{0}.$
Rangul unei matrici
Rangul unei matrici arbitrare este ordinul celui mai mare (în sensul numărului de linii/coloane) determinant nenul ce se poate forma cu elementele matricii date (fără a modifica poziţia lor din liniile/coloanele matricii). Rangul matricii este egal cu $r$, notat $r=\text{rang} A$, dacă matricea admite un minor nenul de ordin $r$, iar toţi minorii de ordin $r+1$, dacă există, sunt nuli.
Matricea cu toate elementele nule are rangul 0 .
Dacă cel puţin un element al matricii $A$ (cu $m$ linii şi $n$ coloane) este nenul atunci rangul verifică inegalitatea
$1 \leq \text{rang} A \leq \min {m, n}.$
Cum se calculează rangul unei matrici?
Dacă $A$ este o matrice pătrată de ordinul $n$ şi $\text{det} A \neq 0$ atunci $\text{rang} A=n$.
Dacă $A$ este o matrice arbitrară sau una pătrată cu $\text{det} A=0$, se procedează în felul următor:
- se fixează un element nenul $a_{i j}$ (dacă este posibil chiar $a_{11}$, elementul din colţul de NV);
- se bordează elementul $a_{i j}$ cu o nouă linie şi o nouă coloană astfel încât determinantul de ordinul al doilea rezultat să fie nenul şi se trece la etapa următoare ( $\text{rang} A \geq 2$ ); dacă prin bordarea lui $a_{i j}$ toţi determinanţii de ordinul doi rezultaţi sunt nuli atunci rang $A=1$ şi calculul s-a încheiat;
- se repetă procedeul descris prin bordarea submatricii de ordinul 2 cu determinant nenul obţinută la etapa precedentă: se caută acum un determinant nenul de ordinul 3; dacă a fost găsit un astfel de determinant, se trece la etapa următoare ( $\text{rang} A \geq 3$ ), iar dacă toţi determinanţii de ordinul 3 construiţi sunt nuli, $\text{rang} A=2$ şi calculul s-a încheiat;
- procedeul poate fi repetat cel mult până se atinge rangul min ${m, n}$ (respectiv $n-1$ în cazul matricilor pătrate).
Inversabilitatea matricilor pătrate. Calculul inversei.
O matrice pătrată $A$ este inversabilă dacă şi numai dacă există o matrice (de acelaşi ordin), notată $A^{-1}$, pentru care $A \cdot A^{-1}=A^{-1} \cdot A=I_n$.
Condiţia necesară şi suficientă ca matricea $A$ să fie inversabilă este
$\text{det} A \neq 0.$
Cum se determină inversa unei matrici $A$ ?
- se calculează $\text{det} A: \text{det} A=0 \Rightarrow A$ nu este inversabilă; $\text{det} A \neq 0 \Rightarrow A$ este inversabilă.
- se calculează transpusa matricei $A=\left[a_{i j}\right]$, matricea $A^t=\left[a_{j i}\right]$ formată cu elementele lui $A$ prin schimbarea liniilor în coloane (păstrând ordinea lor). (Este de remarcat identitatea $\text{det} A=\text{det} A^t$. )
- se calculează reciproca (adjuncta) matricei $A=\left[a_{i j}\right]$, matricea $A^*=\left[\Gamma_{j i}\right]$ formată din complemenţii algebrici ai elementelor transpusei $A^t=\left[a_{j i}\right]$.
- se determină matricea inversă $A^{-1}=\frac{1}{\text{det} A} A^*.$
Sisteme de ecuaţii liniare
Un sistem liniar de $m$ ecuaţii cu $n$ necunoscute are forma
$\begin{cases}a_{11} x_1+a_{12} x_2+\ldots+a_{1 j} x_j+\ldots+a_{1 n} x_n & =b_1 \\ \vdots & \\ a_{i 1} x_1+a_{i 2} x_2+\ldots+a_{i j} x_j+\ldots+a_{i n} x_n & =b_i \\ \vdots & \\ a_{m 1} x_1+a_{m 2} x_2+\ldots+a_{m j} x_j+\ldots+a_{m n} x_n & =b_m\end{cases}$
Echivalent, sistemul poate fi exprimat sub forma matricială $A \cdot X=B$, unde $A=\left[a_{i j}\right]$ reprezintă matricea sistemului şi
$X=\left[\begin{array}{l}x_1 \\ \vdots \\ x_i \\ \vdots \\ x_n\end{array}\right]$, respectiv $B=\left[\begin{array}{l}b_1 \\ \vdots \\ b_i \\ \vdots \\ b_m\end{array}\right].$
Este posibilă numai una dintre următoarele situaţii:
- Sistemul are soluţie unică şi se numeşte compatibil determinat;
- Sistemul admite o infinitate de soluţii şi se numeşte compatibil nedeterminat;
- Sistemul nu are soluţii şi se numeşte incompatibil.
Cazuri particulare
Sistemul Cramer: dacă $A$ este o matrice pătrată ( $m=n$, numărul necunoscutelor coincide cu cel al ecuaţiilor) şi $\text{det} A \neq 0$ atunci sistemul este compatibil determinat, unica sa soluţie, exprimată matricial fiind $X=A^{-1} \cdot B$. Acelaşi rezultat se obţine aplicând regula lui Cramer:
$x_1=\large \frac{\Delta_1}{\text{det} A}, x_2=\large \frac{\Delta_2}{\text{det} A}, \ldots, x_n=\large \frac{\Delta_n}{\text{det} A},$
unde determinanţii $\Delta_k, k=\overline{1, n}$ rezultă din $\Delta=\text{det} A$ prin înlocuirea coloanei $k$ cu cea a termenilor liberi $B$.
Sistemul omogen, sistemul în care toţi termenii liberi sunt nuli $b_i=0$ $(i=\overline{1, m})$. Sistemele omogene sunt compatibile deoarece admit cel puţin soluţia $(0,0, \ldots, 0)$, numită soluţia banală.
Matricea extinsă a sistemului este matricea obţinută prin completarea matricii $A$ cu termenii liberi:
$\bar{A}=(A \mid B)=\left(\begin{array}{ccccc} a_{11} & a_{12} & \ldots & a_{1 n} & \mid b_1 \\ a_{21} & a_{22} & \ldots & a_{2 n} & \mid b_2 \\ \ldots & \ldots & \ldots & \ldots & \mid \ldots \\ a_{m 1} & a_{m 2} & \ldots & a_{m n} & \mid b_m \end{array}\right) .$
Teorema Kronecker-Capelli
Un sistem algebric liniar este compatibil dacă şi numai dacă rangul matricii sistemului coincide curangul matricii extinse a sistemului: $\text{rang} A=\text{rang} \bar{A}$.
Odată calculat rangul matricii $A$ se evidenţiază determinantul principal $\Delta_p$ adică “cel mai mare determinant” nenul ce se poate forma cu elementele matricii $A$. Liniile determinantului principal indică ecuaţiile principale iar coloanele sale, necunoscutele principale; toate celelalte ecuaţii şi necunoscute sunt secundare. Subsistemul format de ecuaţiile principale este un sistem de tip Cramer iar soluţiile sale sunt chiar soluţiile sistemului iniţial.
Determinantul principal poate fi bordat, pe linie, cu coeficienţi situaţi în ecuaţiile secundare şi pe coloană, cu coeficienţi ai necunoscutelor secundare (evident, dacă există ecuaţii şi necunoscute secundare). Determinanţii obţinuţi prin bordare poartă numele de determinanţi (minori) caracteristici.
Teorema lui Rouché
Un sistem de ecuaţii liniare este compatibil dacă toţi minorii caracteristici sunt nuli ( $\text{rang} A<m$ ) sau dacă nu există asemenea minori ( $\text{rang} A=m$ ).
Gradul de nedeterminare al unui sistem compatibil este dat de numărul de necunoscute secundare $n-\text{rang} A>0$; dacă rang $A=n$ atunci sistemul este compatibil determinat (nu există necunoscute secundare).
Un sistem omogen admite soluţii nebanale d.d. dacă rangul matricii sistemului este inferior numărului de necunoscute ( $\text{rang} A<n$ ).
Un sistem omogen în care numărul ecuaţiilor coincide cu numărul necunoscutelor $(m=n)$ admite soluţii nebanale dacă şi numai dacă determinantul matricii sistemului este nul ( $\text{det} A=0$ ).
Structuri algebrice
Definiţie
Fie $M$ o mulțime nevidă; o lege de corespondenţă ce asociază oricărei perechi de elemente $\operatorname{din} M$, în mod unic, un element $\operatorname{din} M$
$$
(x, y) \mapsto x * y: M \times M \rightarrow M
$$
se numeşte lege de compozitie pe $M$.
Simbolul * utilizat pentru a desemna elementul compus $x * y$ este inspirat de cele două tipuri de legi de compoziţie întâlnite din zorii educaţiei matematice, adunarea (+) şi înmulţirea ( $\cdot$ ). În notaţie aditivă, elementul compus se notează prin $x+y$ şi se numeşte sumă iar în notaţie multiplicativă, se notează $x \cdot y$ (uneori scris pe scurt chiar $x y$ ) şi se numeşte produs.
Submulţimea $M_0 \subset M$ este parte stabilă a lui $M$ la legea de compoziţie * dacă şi numai dacă oricărei perechi de elemente $\left(x_0, y_0\right)$ din $M_0 \times M_0$ îi corespunde un element situat de asemenea în $M_0$ :
$$
(\forall) x_0, y_0 \in M_0 \Rightarrow x_0 * y_0 \in M_0
$$
Legea de compoziţie * este asociativă d.d.
$$
(\forall) x, y, z \in M \Rightarrow(x * y) * z=x *(y * z)
$$
Legea de compoziţie * este comutativă d.d.
$$
(\forall) x, y \in M \Rightarrow x * y=y * x
$$
Elementul $e \in M$ se numeşte element neutru pentru legea $*$ dacă
$$
(\forall) x \in M \Rightarrow x * e=e * x=x
$$
Elementul neutru pentru o lege de compoziţie, dacă există, este unic.
Elementul neutru al unei legi de compozitie de tip aditiv este notat prin 0 şi este numit element de efect nul (sau, mai simplu, zero).
Elementul neutru al unei legi de compoziţie de tip multiplicativ este notat prin 1 şi este numit element unitate.
Un element $x$ se numeşte simetrizabil în raport cu legea $*$ dacă
$$
\text { (ヨ) } x^{\prime} \in M \text { a.î. } x * x^{\prime}=x^{\prime} * x=e \text {. }
$$
Elementul notat prin $x^{\prime}$ este simetricul lui $x$.
Dacă elementele $x, y$ şi $z$ sunt simetrizabile atunci $x * y$ şi $z^{\prime}$ sunt şi ele simetrizabile. În plus, sunt verificate identităţile
$$
(x * y)^{\prime}=y^{\prime} * x^{\prime} \quad \text { şi } \quad\left(z^{\prime}\right)^{\prime}=z
$$
Simetricul lui $x$ în raport cu o lege de compoziţie de tip aditiv este notat prin $-x$ şi este numit opusul lui $x$.
Simetricul lui $x$ în raport cu o lege de compoziţie de tip multiplicativ este notat prin $x^{-1}$ şi este numit inversul lui $x$.
Definiţie
Mulțimea nevidă $M$, înzestrată cu legea de compoziţie $*$ , este monoid dacă şi numai dacă legea $*$ este asociativă şi are element neutru:
$$
\begin{aligned}
& (\forall) x, y, z \in M \Rightarrow(x * y) * z=x *(y * z) \\
& (\exists) e \in M \text { a.î. }(\forall) x \in M \Rightarrow x * e=e * x=x .
\end{aligned}
$$
Dacă legea de compoziţie este comutativă atunci $M$ este un monoid comutativ.
Definiţie
Mulţimea nevidă $G$, înzestrată cu legea de compoziţie *, este grup dacă legea * este asociativă, are element neutru şi toate elementele din $G$ sunt simetrizabile.
Aşadar, $(G, *)$ este grup d.d. sunt satisfăcute următoarele axiome:
$$
\begin{aligned}
& (\forall) x, y, z \in G \Rightarrow(x * y) * z=x *(y * z); \\
& (\exists) e \in G \text{ a.î. } (\forall) x \in G \Rightarrow x * e=e * x=x; \\
& (\forall) x \in G (\exists) x^{\prime} \in G \text{ a.î. } x * x^{\prime}=x^{\prime} * x=e.
\end{aligned}
$$
Dacă legea de compoziţie este comutativă atunci ( $G, *$ ) este un grup comutativ sau abelian.
Teoremă
Fie ( $G, *$ ) un grup şi $a, b \in G$ două elemente arbitrare în $G$. Ecuaţiile $a * x=b \quad$ şi $\quad y * a=b$ au soluţii unice în $G$, mai precis
$$
\begin{array}{lll}
a * x=b & \Longleftrightarrow x=a^{\prime} * b & \text { respectiv } \
y * a=b & \Longleftrightarrow y=b * a^{\prime} &
\end{array}
$$
Dacă $(G,+)$ este un grup în care legea de compoziţie este de tip aditiv atunci pentru orice $a \in G$ şi orice numere intregi $m, n$, au loc identităţile:
$$
m a+n a=(m+n) a, \quad m(n a)=(m n) a, \quad-(n a)=n(-a), \quad 0 a=0
$$
Dacă ( $G, \cdot$ ) este un grup în care legea de compoziţie este de tip multiplicativ atunci pentru orice $a \in G$ şi orice numere întregi $m, n$, au loc identităţile
$$
a^m \cdot a^n=a^{m+n}, \quad\left(a^m\right)^n=a^{m n}, \quad\left(a^n\right)^{-1}=a^{-n} \quad a^0=1
$$
Definiţie
O submulţime nevidă $H \subset G$ a unui grup ( $G, *$ ) se numeşte subgrup al lui $G$ dacă sunt satisfăcute următoarele condiţii
$(\forall) x, y \in H \Rightarrow x * y \in H$;
( $\forall$ ) $x \in H \Rightarrow x^{\prime} \in H$.
Definiţie
Fie $\left(G_1, *\right)$ şi $\left(G_2\right.$, o $)$ două grupuri; funcţia bijectivă $f: G_1 \rightarrow G_2$ se numeşte izomorfim de grupuri dacă
$f(x * y)=f(x) \circ f(y) \quad(\forall) x, y \in G_1$
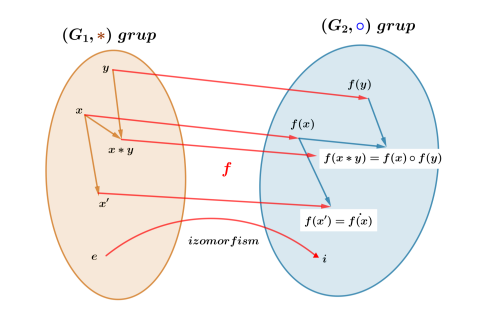
Exemplu
Funcţia logaritm natural $\ln :(0,+\infty) \rightarrow \mathbb{R}$ realizează un izomorfism între $((0,+\infty), \cdot)$, grupul multiplicativ al numerelor pozitive şi $(\mathbb{R},+)$, grupul aditiv al numerelor reale. Într-adevăr, ln este bijectivă şi satisface condiţia
$$
\ln (x \cdot y)=\ln x+\ln y
$$
Definiţie
- O mulţime nevidă $A$ înzestrată cu două legi de compoziţie, una aditivă şi una multiplicativă, notate tradiţional + şi $\cdot$, se numeşte inel dacă sunt satisfăcute următoarele axiome:
- $ (A,+)$ este grup comutativ,
- $ (A, \cdot)$ este monoid,
- înmulţirea $(\cdot)$ este distributivă faţă de adunare $(+)$, mai precis $ (\forall) x, y, z \in A \quad x(y+z)=x y+x z$ şi $(y+z) x=y x+z x.$
Dacă înmulţirea elementelor $\text{din } A$ este o lege de compoziţie comutativă atunci inelul ( $A,+, \cdot$ ) este un inel comutativ.
Inelul $(A,+, \cdot)$ este un inel fără divizori ai lui zero dacă
$$
x \neq 0 \quad \text { şi } y \neq 0 \Rightarrow x y \neq 0 .
$$
Un inel comutativ (format din cel puţin două elemente) fără divizori ai lui zero se numeşte domeniu de integritate.
Elementele nenule $u, v \in A$ sunt divizori ai lui zero dacă $u v=0$.
Exemplu
Inelul numerelor intregi ( $\mathbb{Z},+, \cdot$ ) este domeniu de integritate. Singurele elemente inversabile (adică simetrizabile faţă de operaţia multiplicativă •) sunt 1 şi -1.
Definiţie
Fie $\left(A_1,+, \cdot\right)$ şi $\left(A_2,+, \cdot\right)$ două inele (fiecare înzestrată cu propriile sale legi de compoziţie, deşi acestea sunt notate similar); funcţia bijectivă $f: A_1 \rightarrow A_2$ se numeşte izomorfim de inele dacă
$$
\begin{aligned}
f(x+y) & =f(x)+f(y) \\
f(x \cdot y) & =f(x) \cdot f(y)
\end{aligned} \quad(\forall) x, y \in A_1
$$
Definiţie
Un inel ( $K,+, \cdot$ ) se numeşte corp dacă $0 \neq 1$ şi orice element nenul $x$ este inversabil.
Exemple
Mulţimile numerice $\mathbb{Q}, \mathbb{R}$ şi $\mathbb{C}$ sunt corpuri comutative.
$\mathbb{Z}_p$, inelul claselor de resturi modulo $p,$ $p$ număr prim.
Fie $n$ un număr întreg arbitrar şi $p$ un număr natural fixat; conform teoremei împărţirii cu rest, există doi întregi, $q$ şi $r$ unic determinaţi, astfel încât
$$
n=q p+r \quad \text { cu } \quad 0 \leq r<p
$$
Numărul $q$ se numeşte cât al împărţirii $n: p$ iar $r$ se numeşte rest. Resturile posibile la împărţirea $n: p$ sunt $0,1,2, \ldots, p-1$. Astfel mulţimea numerelor întregi $\mathbb{Z}$ se poate descompune în $p$ submulţimi disjuncte:
$\begin{aligned}{\ldots,-p, \boxed{0}, p, 2 p, \ldots}= & {k p \mid k \in \mathbb{Z}} \stackrel{\text { not }}{=} \widehat{0}, \\ {\ldots,-p+1, \boxed{1}, p+1,2 p+1, \ldots}= & {k p+1 \mid k \in \mathbb{Z}} \stackrel{\text { not }}{=} \widehat{1}, \\ & \vdots \\ {\ldots,-p+r, \boxed{r}, p+r, 2 p+r, \ldots}= & {k p+r \mid k \in \mathbb{Z}} \stackrel{\text { not }}{=} \widehat{r}, \\ & \vdots \\ {\ldots,-p+(p-1), \boxed{p-1}, p+(p-1), \ldots}= & {k p+(p-1) \mid k \in \mathbb{Z}} \stackrel{\text { not }}{=} \widehat{p-1},\end{aligned}$
numite clase de resturi modulo $p$. Mulţimea tuturor claselor de resturi modulo $p$ se notează $\mathbb{Z}_p$ :
$$
\mathbb{Z}_p={\widehat{0}, \widehat{1}, \widehat{2}, \ldots, \widehat{p-1}}
$$
Pe această mulţime se introduc două legi de compoziţie după cum urmează: adunarea claselor modulo $p, \quad \widehat{a}+\widehat{b} \stackrel{\text { def }}{=} \widehat{a+b} \quad$ şi înmulţirea claselor modulo $p, \quad \widehat{a} \cdot \widehat{b} \stackrel{\text { def }}{=} \widehat{a \cdot b}$.
Adunarea şi înmulţirea sunt corect definite deoarece, conform definiției claselor de resturi, dacă întregul $k \in \widehat{r}$ şi $0 \leq r<p$ atunci $\widehat{k}=\widehat{r}$.
$\left(\mathbb{Z}_p,+, \cdot\right)$ este inel comutativ în care elementul neutru la adunare este $\widehat{0}$ iar elementul neutru la înmulţire este $\widehat{1}$.
Orice clasă de resturi $\widehat{a} \in \mathbb{Z}_p$ are opus: $-\widehat{a}=\widehat{p-a}$.
Nu toate clasele de resturi din $\mathbb{Z}_p$ sunt inversabile: elementul $\widehat{a} \in \mathbb{Z}_p$ este inversabil d.d. singurul divizor comun al lui $a$ şi $p$ este 1 .
În consecinţă, dacă $a$ este divizor propriu al lui $p(a \neq 1$ şi $a \neq p)$ atunci $p=a b$ iar $\widehat{a} \cdot \widehat{b}=\widehat{p}=\widehat{0}$ deci $\widehat{a}$ este divizor al lui zero.
i) Dacă $p$ este neprim atunci $\left(\mathbb{Z}_p,+, \cdot\right)$ este inel cu divizori ai lui zero.
ii) Dacă $p$ este un număr prim atunci toate elementele din $\mathbb{Z}_p \backslash{\widehat{0}}$ sunt inversabile ceea ce conferă lui $\left(\mathbb{Z}_p,+, \cdot\right)$ o structură de corp comutativ.
iii) Dacă $p$ este un număr prim atunci $\widehat{a}^{p-1}=\widehat{1}$ oricare ar fi $\widehat{a} \in \mathbb{Z}_p \backslash{\widehat{0}}.$