Cuprins
Limite de funcţii şi funcţii continue
Aplicaţiile derivatei (puncte de extrem, șirul lui Rolle, regula lui l’Hospital)
Ghid pentru reprezentarea grafică a funcţiilor
Integrabilitate şi aplicaţii (arii și volume)
Şiruri de numere reale
O funcţie reală $f$ definită pe mulţimea numerelor naturale $\mathbb{N}$ (sau, echivalent, pe o secţiune $\mathbb{N}m$ a sa ce cuprinde toate numerele naturale ce depăşesc o valoare fixată $m$ ) se numeşte şir de numere reale. Este convenabilă precizarea şirului prin intermediul termenului său general: $f(n)=a_n \quad(n \in \mathbb{N})$ utilizând simplu notaţia $\left(a_n\right){n \in \mathbb{N}}$;
Şirul $\left(a_n\right){n \in \mathbb{N}}$ este monoton dacă şi numai dacă $\text{sgn}\left(a_{n+1}-a_n\right)$ este constant oricare ar fi $n \in \mathbb{N}$.
$a_{n+1}-a_n \gt 0 \quad(\forall) n \in \mathbb{N} \Rightarrow\left(a_n\right)$ este strict crescător
$a_{n+1}-a_n \lt 0 \quad(\forall) n \in \mathbb{N} \Rightarrow\left(a_n\right)$ este strict descrescător
Şirul $\left(a_n\right)_{n \in \mathbb{N}}$ este mărginit dacă şi numai dacă toţi termenii săi se găsesc într-un interval mărginit:
$(\exists) M \gt 0$ a. î. $(\forall) n \in \mathbb{N}, \quad\left|a_n\right| \leq M$.
Definiţie
Şirul de numere reale $\left(a_n\right){n \in \mathbb{N}}$ este convergent dacă există un număr real $l$ cu proprietatea că pentru orice $\varepsilon>0$ există un rang $n{\varepsilon}$ astfel încât, pentru orice $n \geq n_{\varepsilon}$, are loc inegalitatea $\left|a_n-l\right|<\varepsilon$; spunem că numărul real $l$ este limita şirului cu termenul general $a_n$ şi notăm aceasta prin $l=\lim \limits _{n \rightarrow \infty} a_n$ sau $a_n \rightarrow l$.
Şirul de numere reale $\left(a_n\right)_{n \in \mathbb{N}}$ are limita $+\infty(-\infty)$ dacă pentru orice număr $M \gt 0$ se poate preciza un rang $n_M$ astfel încât, pentru orice $n \geq n_M$, are loc inegalitatea $a_n \gt M\left(a_n \lt -M\right)$.
Şirurile care au limita infinită sau cele pentru care limita nu există se numesc divergente.
Теогеmă
Fie $\left(a_n\right)n$ şi $\left(b_n\right){n \in \mathbb{N}}$ două şiruri convergente având aceeaşi limită $l$ iar $\left(x_n\right)_n$ este un alt şir care verifică dubla inegalitate:
$$
a_n \leq x_n \leq b_n \text { oricare ar fi } n \geq n^{\prime}
$$
atunci $\left(x_n\right){n \in \mathbb{N}}$ este convergent iar $\lim \limits_ {n \rightarrow \infty} x_n=l$.
Consecinţa 1
Fie $\left(b_n\right)_n$ un şir convergent având limita 0 şi $\left(x_n\right)_n$ un alt şir pentru care există numărul real $l$ cu proprietatea
$$
\left|x_n-l\right| \lt b_n \text { pentru orice rang } n \geq n^{\prime}
$$
atunci şi $\left(x_n\right)n$ este convergent iar $\lim \limits_ {n \rightarrow \infty} x_n=l$.
Consecinţa 2
Fie şirul $\left(x_n\right)n$ cu termenul general de forma $x_n=a_n \cdot b_n$;
dacă $\left(a_n\right)_n$ este un şir mărginit iar $\left(b_n\right)_n$ unul convergent cu limita 0 atunci $\lim \limits_{n \rightarrow \infty} x_n=0$.
Proprietăţile şirurilor convergente
i) Limita unui şir convergent de numere reale este unică.
ii) Orice şir convergent de numere reale este mărginit:
$$
\lim _{n \rightarrow \infty} a_n=l \Rightarrow \left (\exists \right) A, B \in \mathbb{R} \text { a.î. }(\forall) n \geq n^{\prime}, a_n \in[A, B] .
$$
Теогеmă
Orice şir monoton şi mărginit este convergent.
Reciproca este falsă: şirul $\left(\large \frac{(-1)^{n+1}}{n}\right)_{n \geq 1}$ este convergent (cu limita 0 ) dar nu este monoton.
Limite remarcabile
$\lim \limits_{n \rightarrow \infty} \frac{1}{n^r}= \begin{cases}0, & r>0 \\ 1, & r=0\end{cases}\qquad\qquad \lim \limits_{n \rightarrow \infty} q^n= \begin{cases}0, & |q| \lt 1 \\ 1, & q=1 \\ \infty, & q \gt 1\end{cases}$
$\lim \limits_{n \rightarrow \infty}\left(a_0 n^p+a_1 n^{p-1}+\cdots+a_p\right)= \begin{cases}-\infty, & a_0 \lt 0 \\ +\infty, & a_0 \gt 0\end{cases}$
$\lim \limits_{n \rightarrow \infty} \large \frac{a_0 n^p+a_1 n^{p-1}+\cdots+a_p}{b_0 n^q+b_1 n^{q-1}+\cdots+b_q}\normalsize =\begin{cases}0, & p \lt q \\ \large \frac{a_0}{b_0} \normalsize, & p=q \\ \infty \cdot \text{sgn}\large \frac{a_0}{b_0} \normalsize, & p \gt q\end{cases}$
$\lim \limits_{n \rightarrow \infty} \large \frac{n}{a^n}\normalsize=0 \quad(|a| \gt 1) \qquad \qquad \lim \limits_{n \rightarrow \infty} \large \frac{a^n}{n!}\normalsize=0 \quad(a \in \mathbb{R})$
$\lim \limits_{n \rightarrow \infty} \frac{\ln n}{n^r}=0 \quad(r>0) \qquad \qquad \lim \limits_{n \rightarrow \infty} \sqrt[n]{n}=1$
Şirul cu termenul general $e_n=\left(1+\large\frac{1}{n}\normalsize\right)^n$ este crescător şi mărginit în intervalul $[2,3]$.
Şirul cu termenul general $E_n=1+\large\frac{1}{1!}\normalsize+\large\frac{1}{2!}\normalsize+\cdots+\large\frac{1}{n!}\normalsize$ este crescător şi verifică inegalităţile
$2 \lt e_n \lt E_n \lt e \lt 3$
$\lim \limits _{n \rightarrow \infty}\left(1+\large\frac{1}{n}\normalsize\right)^n=e \qquad \qquad \lim \limits _{n \rightarrow \infty}\left(1+\large\frac{1}{1!}\normalsize+\large\frac{1}{2!}\normalsize+\cdots+\large\frac{1}{n!}\normalsize\right)=e$
Numărul $e \simeq 2,718281 \ldots$ este baza logaritmului natural: $\ln e=1$.
Limite de funcţii şi funcţii continue
Fie $D \subset \mathbb{R}$ o mulţime nevidă şi $a \in \overline{\mathbb{R}}=\mathbb{R} \cup{ \pm \infty}$ un punct de acumulare al acesteia adică un punct pentru care există şiruri $\left(x_n\right)_n \text{ din } D, x_n \neq a$ a.î. $\lim \limits_ {n \rightarrow \infty} x_n=a.$
Definiţie
Funcţia $f: D \rightarrow \mathbb{R}$ are limita $l$ (finită sau infinită) în punctul $a$ dacă pentru orice şir $\left(x_n\right)_n \text{ din } D, x_n \neq a$ cu $\lim \limits_ {n \rightarrow \infty} x_n=a$ este verificată egalitatea $\lim \limits_{n \rightarrow \infty} f\left(x_n\right)=l$. Notăm aceasta prin $\lim \limits_{x \rightarrow a} f(x)=l$.
Limita unei funcţii într-un punct (de acumulare al domeniului de definiţie), dacă există, este unică.
Dacă există două şiruri $\left(x_n^{\prime}\right)_n$ şi $\left(x_n^{\prime \prime}\right)_n$ in $D, x_n^{\prime}, x_n^{\prime \prime} \neq a$ cu $\lim \limits_{n \rightarrow \infty} x_n^{\prime}=$ $\lim \limits_{n \rightarrow \infty} x_n^{\prime \prime}=a~$ dar $~\lim \limits_{n \rightarrow \infty} f\left(x_n^{\prime}\right) \neq \lim \limits _{n \rightarrow \infty} f\left(x_n^{\prime \prime}\right)$ atunci funcţia $f$ nu are limită în punctul $a.$
Exemple
- $\lim \limits_ {x \rightarrow \infty} \sin x$ nu există deoarece pentru şirurile $(n \pi)_n$ şi $\left((4 n+1) \frac{\pi}{2}\right)_n$ cu $\lim \limits_ {n \rightarrow \infty} n \pi=\lim \limits_ {n \rightarrow \infty}(4 n+1) \frac{\pi}{2}=\infty$, şirurile valorilor funcţiei au limite diferite, $\lim \limits_ {n \rightarrow \infty} \sin n \pi=\lim \limits_ {n \rightarrow \infty} 0=0$, în timp ce
$$
\lim \limits_ {n \rightarrow \infty} \sin (4 n+1) \frac{\pi}{2}=\lim \limits_ {n \rightarrow \infty} \sin \left(2 n \pi+\frac{\pi}{2}\right)=\lim \limits_ {n \rightarrow \infty} \sin \left(\frac{\pi}{2}\right)=\lim \limits_ {n \rightarrow \infty} 1=1
$$
- $\lim \limits_ {x \rightarrow 0} \sin \frac{1}{x}$ nu există deoarece pentru şirurile $\left(\frac{1}{n \pi}\right)_n$ şi $\left(\frac{2}{(4 n+1) \pi}\right)_n$ cu $\lim \limits_ {n \rightarrow \infty} \frac{1}{n \pi}=\lim \limits_ {n \rightarrow \infty} \frac{2}{(4 n+1) \pi}=0$, şirurile valorilor funcţiei au limite diferite, $\lim \limits_ {n \rightarrow \infty} \sin \frac{1}{\frac{1}{n \pi}}=\lim \limits _{n \rightarrow \infty} \sin n \pi=0$, în timp ce
$$
\lim \limits_ {n \rightarrow \infty} \sin \frac{1}{\frac{2}{(4 n+1) \pi}}=\lim \limits_ {n \rightarrow \infty} \sin (4 n+1) \frac{\pi}{2}=1
$$
Limite laterale:
$\lim \limits _{\substack{x \rightarrow a \\ x \lt a}} f(x) \stackrel{\text { not }}{=} f(a-0)$ (limita la stânga) şi $\lim \limits _{\substack{x \rightarrow a \\ x \gt a}} f(x) \stackrel{\text { not }}{=} f(a+0)$ (limita la dreapta).
Dacă $f$ are limite laterale egale $f(a-0)=f(a+0)=l$ atunci $f$ are limită în $a$ şi $\lim \limits _{x \rightarrow a} f(x)=l$.
Dacă $f$ are limite laterale diferite $f(a-0) \neq f(a+0)$ atunci $f$ nu are limită în $a(\lim \limits _{x \rightarrow a} f(x)$ nu există $)$.
Теоrеmӑ
Fie $f, g: D \rightarrow \mathbb{R}$ două funcţii, $a$ un punct de acumulare al domeniului $D$, $V_a$ o vecinătate a lui $a$ şi $l$ un număr real.
Dacă
i) $\lim _{x \rightarrow a} g(x)=0$
atunci $f$ are limită în $a$ şi
ii) $|f(x)-l| \leq|g(x)|$
$(\forall) x \in V_a \cap D$ $\lim _{x \rightarrow a} f(x)=l$.
Exemplu
$$
\lim \limits _{x \rightarrow 0} x \sin \frac{1}{x}=0 \text { deoarece }\left|x \sin \frac{1}{x}-0\right|=|x| \cdot\left|\sin \frac{1}{x}\right| \leq|x| \cdot 1=|x|.
$$
Limite remarcabile
$$
\lim _{x \rightarrow \pm \infty} \frac{a_0 x^p+a_1 x^{p-1}+\cdots+a_p}{b_0 x^q+b_1 x^{q-1}+\cdots+b_q}= \begin{cases}0, & p \lt q \\ \frac{a_0}{b_0}, & p=q \\ \frac{a_0}{b_0}( \pm \infty)^{p-q}, & p \gt q\end{cases}
$$
$$
\lim\limits_ {x \rightarrow \infty} x a^{-x}=0 \quad(a \gt 1); \quad \lim\limits_ {x \rightarrow \infty} \frac{\ln x}{x^r}=0; \quad \lim\limits _{\substack{x \rightarrow 0 \ x \gt 0}} \frac{x^r}{\ln x}=0 \quad(r \gt 0)
$$
$$
\lim\limits_ {x \rightarrow 0}(1+x)^{\frac{1}{x}}=e; \quad \lim\limits_ {x \rightarrow 0} \frac{\ln (1+x)}{x}=1
$$
$$
\lim\limits_ {x \rightarrow 0} \frac{a^x-1}{x}=\ln a; \quad \lim\limits_ {x \rightarrow 0} \frac{(1+x)^r-1}{x}=r
$$
$$
\lim\limits_ {x \rightarrow 0} \frac{\sin x}{x}=1; \quad \lim\limits_ {x \rightarrow 0} \frac{1-\cos x}{x^2}=\frac{1}{2}; \quad \lim\limits _{x \rightarrow 0} \frac{\text{tg} x}{x}=1
$$
$$
\lim\limits_ {x \rightarrow 0} \frac{\arcsin x}{x}=1; \quad \lim\limits_ {x \rightarrow 0} \frac{\frac{\pi}{2}-\arccos x}{x}=1; \quad \lim\limits _{x \rightarrow 0} \frac{\text{arctg} x}{x}=1
$$
Fie $D \subset \mathbb{R}$ o mulţime nevidă şi $a \in D$ un punct de acumulare al domeniului de definiție.
Definiţie
Funcţia $f: D \rightarrow \mathbb{R}$ este continuă în $a$ dacă $\lim\limits_ {x \rightarrow a} f(x)$ există şi coincide cu valoarea funcţiei în $a$, mai precis $\lim\limits_ {x \rightarrow a} f(x)=f(a)$.
Funcţia $f: D \rightarrow \mathbb{R}$ este continuă pe mulţimea $D_0 \subset D$ dacă este continuă în fiecare punct al mulțimii $D_0$.
Punctele de acumulare ale domeniului în care funcţia nu este continuă se numesc puncte de discontinuitate.
Funcţia $f$ prezintă o discontinuitate de speţa intâi în $x=a$ dacă are limite laterale finite şi diferite în $a(f(a-0) \neq f(a+0))$ sau acestea sunt finite egale dar diferite de $f(a)$. Orice punct de discontinuitate care nu este de speţa întâi este clasificat de speţa a doua.
Exemplu
Funcţia $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)= \begin{cases}\sin \frac{1}{x}, & x \neq 0 \\ 0, & x=0\end{cases}$ este discontinuă în $a=0$; punctul $a=0$ este punct de discontinuitate de speţa a doua.
Proprietăţi ale functiilor continue
- Orice funcţie continuă pe un interval mărginit şi închis este mărginită şi îşi atinge marginile. Mai precis, oricare ar fi $x \in[a, b]$ toate valorile $f(x)$ se găsesc în intervalul $[m, M]$ ( $m$ şi $M$ reprezintă minimul, respectiv maximul funcţiei) şi în plus, există $x_m \in[a, b]$ şi $x_M \in[a, b]$ aşa încât $m=f\left(x_m\right)$ şi respectiv, $M=f\left(x_M\right)$.
- Dacă $f:[a, b] \rightarrow \mathbb{R}$ este continuă şi ia valori de semne diferite în capetele intervalului $[a, b]$ atunci ecuaţia $f(x)=0$ are cel puţin o rădăcină în intervalul $(a, b)$.
- Dacă $f: I \rightarrow \mathbb{R}$ este continuă pe intervalul $I$ atunci imaginea acestuia $J=f(I)(=\text{Im}(f))$ este de asemenea un interval.
Observaţii asupra proprietăţii lui Darboux
O funcţie $f: I \rightarrow \mathbb{R}$ are proprietatea lui Darboux dacă oricare ar fi $a, b \in I$ $(a \lt b)$ şi $\lambda$ situat intre $f(a)$ şi $f(b)$ există cel puţin un punct $c_\lambda \in(a, b)$ pentru care $\lambda=f\left(c_\lambda\right)$.
Orice funcţie continuă pe un interval are proprietatea lui Darboux.
Funcţiile discontinue care prezintă o discontinuitate de speţa întâi nu au proprietatea lui Darboux.
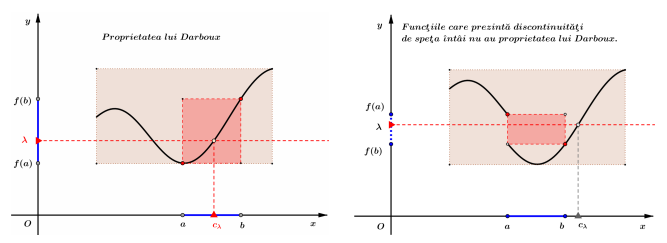
Funcţia $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)= \begin{cases}\sin \frac{1}{x}, & x \neq 0 \\ 0, & x=0\end{cases}$ are proprietatea lui Darboux deşi este discontinuă (discontinuitatea este de speţa a doua!).
Funcţii derivabile
Definiţie
O funcţie $f: I \rightarrow \mathbb{R}$ este derivabilă in punctul $a$ (situat in intervalul $I$ ) dacă limita $\lim \limits _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}$ există şi este finită.
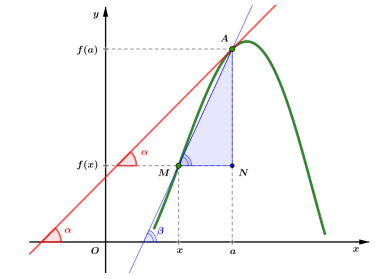
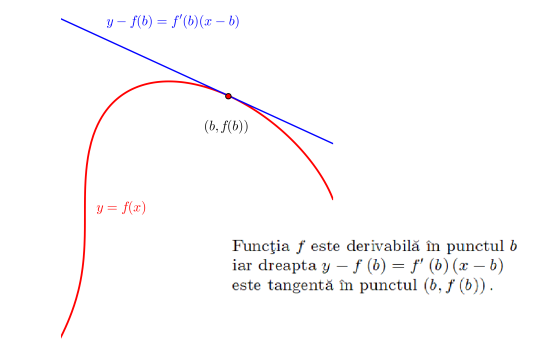
Interpretarea geometrică a derivatei
Din punct de vedere geometric, raportul $\frac{f(x)-f(a)}{x-a}$ este tangenta unghiului $\widehat{A M N}$ (vezi figura) şi urmare a trecerii la limită după $x \rightarrow a, f^{\prime}(a)$ nu reprezintă altceva decât panta tangentei la graficul funcţiei $f$ în punctul $A(a, f(a)) . \mathrm{Cu}$ alte cuvinte, $f^{\prime}(a)$ este tangenta (trigonometrică a) unghiului pe care dreapta tangentă în punctul $A$ îl face cu semiaxa pozitivă $O x$. Ecuaţia tangentei la graficul funcţiei $f$ în punctul de abscisă $a$ este
$$
y-f(a)=f^{\prime}(a)(x-a)
$$
Uneori, pentru a pune în evidenţă şi variabila independentă a funcţiei, numărul $f^{\prime}(a)$, derivata lui $f$ in $x=a$ se notează prin $\frac{d f}{d x}(a)$ iar derivata $f^{\prime}(x)$ într-un punct arbitrar pur şi simplu prin $\frac{d f}{d x}$.
O interpretare fizică a derivatei
Un mobil aflat în mişcare rectilinie parcurge în $t$ unităţi de timp (secunde / minute / ore) distanţa $s(t)$ (măsurată în metri / kilometri) sau, cu alte cuvinte, distanţa parcursă de mobil poate fi privită ca o funcţie $s:[0, T] \rightarrow \mathbb{R}$. Dacă $s$ este derivabilă pe $[0, T]$ atunci viteza sa la momentul $t$ se defineşte prin $v(t)=s^{\prime}(t)$ iar dacă şi $v$ este o funcţie derivabilă atunci acceleraţia mobilului la momentul $t$ este $a(t)=v^{\prime}(t)=s^{\prime \prime}(t)$.
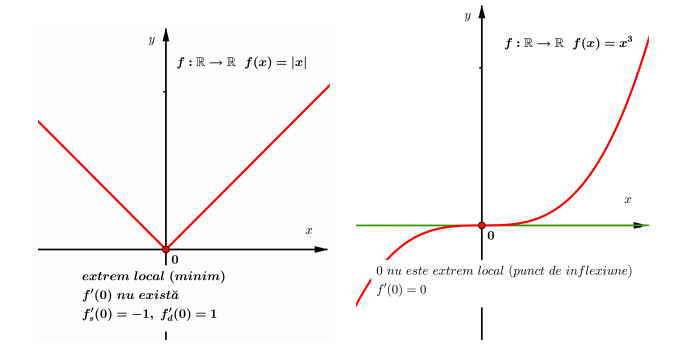
Condiţia necesară de derivabilitate
Orice funcţie derivabilă într-un punct este continuă în acel punct. Reciproca afirmaţiei este falsă: spre exemplu funcţia modul este continuă în origine fără a fi însă derivabilă.
Cum se studiază derivabilitatea unei funcfii într-un punct?
- se verifică proprietatea de continuitate în punctul precizat (dacă funcţia este discontinuă studiul derivabilităţii nu are sens),
- se calculează derivatele laterale
$$
f_s^{\prime}(a)=\lim _{\substack{x \rightarrow a \\ x \lt a}} \frac{f(x)-f(a)}{x-a} \text{ și } f_d^{\prime}(a)=\lim _{\substack{x \rightarrow a \\ x \gt a}} \frac{f(x)-f(a)}{x-a}
$$
Dacă derivatele laterale în $a$ există, sunt finite şi egale atunci funcţia $f$ este derivabilă în $a$. (Pentru punctele situate la extremităţile -finite- ale domeniului de definiție este suficient ca una singură din derivatele laterale să existe şi să fie finită). În toate celelalte situaţii, funcţia nu este derivabilă în punctul studiat.
Tabelul derivatelor
Identităţile din tabelele ce urmează se deduc cu formula
$$
f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}
$$
ce rezultă din definiţie prin schimbarea de variabilă $x-a=h$.
$$
\begin{array}{|l|l|l|l|}
\hline 1. & f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=x^n & \left(x^n\right)^{\prime}=n x^{n-1} & (n \in \mathbb{N})\\
\hline & f: \mathbb{R}^* \rightarrow \mathbb{R}, f(x)=\frac{1}{x^n}& \left(\frac{1}{x^n}\right)^{\prime}=-\frac{n}{x^{n+1}}& (n \in \mathbb{N})\\
\hline & & \left(\frac{1}{x}\right)^{\prime}=-\frac{1}{x^2} & \\
\hline & f:(0, \infty) \rightarrow \mathbb{R}, f(x)=x^r& \left(x^r\right)^{\prime}=r x^{r-1} & (r \in \mathbb{R})\\
\hline & & (\sqrt{x})^{\prime}=\frac{1}{2 \sqrt{x}} & \\
\hline & & (\sqrt[3]{x})^{\prime}=\frac{1}{3 \sqrt[3]{x^2}}& \\
\hline 2 . & f: \mathbb{R} \rightarrow(0, \infty), f(x)=a^x & \left(a^x\right)^{\prime}=a^x \ln a & (a \gt 0, a \neq 1) \\
\hline & & \left(e^x\right)^{\prime}=e^x \\
\hline 3 . & f:(0, \infty) \rightarrow \mathbb{R}, f(x)=\log _a x & \left(\log _a x\right)^{\prime}=\frac{1}{x \ln a} & (a \gt 0, a \neq 1) \\
\hline && (\ln x)^{\prime}=\frac{1}{x} & \\
\hline && (\ln |x|)^{\prime}=\frac{1}{x} & (x \neq 0) \\
\hline 4. & f: \mathbb{R} \rightarrow[-1,1], f(x)=\sin x & (\sin x)^{\prime}=\cos x \\
\hline 5. & f: \mathbb{R} \rightarrow[-1,1], f(x)=\cos x & (\cos x)^{\prime}=-\sin x \\
\hline 6. & f: \mathbb{R} \backslash\left \{(2 k+1) \frac{\pi}{2}\right \}_{k \in \mathbb{Z}} \rightarrow \mathbb{R}, f(x)=\text{tg} x & (\text{tg} x)^{\prime}=\frac{1}{\cos ^2 x} \\
\hline & & (\text{tg} x)^{\prime}=1+\text{tg}^2 x \\
\hline 7. & f: \mathbb{R} \backslash{k \pi}_{k \in \mathbb{Z}} \rightarrow \mathbb{R}, f(x)=\text{ctg} x & (\text{ctg} x)^{\prime}=\frac{-1}{\sin ^2 x} \\
\hline 8 . & f:[-1,1] \rightarrow\left[-\frac{\pi}{2}, \frac{\pi}{2}\right], f(x)=\arcsin x & (\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^2}} & (x \neq \pm 1) \\
\hline 9 . & f:[-1,1] \rightarrow[0, \pi], f(x)=\arccos x & (\arccos x)^{\prime}=\frac{-1}{\sqrt{1-x^2}} & (x \neq \pm 1) \\
\hline 10 . & f: \mathbb{R} \rightarrow\left(-\frac{\pi}{2}, \frac{\pi}{2}\right), f(x)=\text{arctg} x & (\text{arctg} x)^{\prime}=\frac{1}{x^2+1} & \\
\hline
\hline
\end{array}
$$
Proprietăţi ale funcţiilor derivabile
$$
\begin{array}{|lll|}
\hline(f(x)+g(x))^{\prime} & =f^{\prime}(x)+g^{\prime}(x) \\
\hline(f(x) \cdot g(x))^{\prime} & =f^{\prime}(x) g(x)+f(x) g^{\prime}(x) \\
\hline\left(\large\frac{f(x)}{g(x)}\right)^{\prime} & =\large \frac{f^{\prime}(x) g(x)-f(x) g^{\prime}(x)}{g^2(x)}, g(x) \neq 0 \\
\hline \left(\large \frac{1}{g(x)}\right)^{\prime} & =\large \frac{-g^{\prime}(x)}{g^2(x)}, & g(x) \neq 0 \\
\hline(f(u(x)))^{\prime} & =f^{\prime}(u(x)) \cdot u^{\prime}(x) \\
\hline
\end{array}
$$
Dacă $f: I \subseteq \mathbb{R} \rightarrow \mathbb{R}$ este o funcţie derivabilă pe intervalul $I$ atunci derivata sa $f^{\prime}$ are proprietatea lui Darboux pe $I$.
Derivate de ordin superior
O funcţie reală este de clasă $\mathcal{C}^1$ pe intervalul $I \subset \mathbb{R}$ dacă este derivabilă în fiecare punct din $I$ şi în plus, derivata sa $f^{\prime}$ este continuă pe $I$. Mulțimea funcţiilor de clasă $\mathcal{C}^1$ pe $I$ se noteză cu $\mathcal{C}_I^1$ iar $\mathcal{C}_I^0$ desemnează în mod natural clasa funcţiilor continue pe intervalul $I$.
În general, pentru un indice $n \in \mathbb{N}$ fixat, se spune că $f$ este o funcţie de clasă $\mathcal{C}^n$ (notaţie $f \in \mathcal{C}_I^n$ ) dacă $f$ e derivabilă de $n$ ori pe $I$ cu derivata $f^{(n)}$ continuă.
Funcţiile elementare cum ar fi $e^x, \cos x, \sin x$, polinoamele de orice grad, logaritmul (indiferent de bază) sunt funcţii de clasă $\mathcal{C}^{\infty}$ pe domeniul lor maxim de definiţie $I$.
Tabelul derivatelor de ordinul $n$
$$
\begin{array}{|l|l|}
\hline \left(x^p\right)^{(n)} & p \geq n, \quad(p \in \mathbb{N}), \quad p \lt n, \quad(p \in \mathbb{N})$ \\
\hline \left(\frac{1}{x}\right)^{(n)}=\frac{(-1)^n n!}{x^{n+1}} & ( x \neq 0) \\
\hline \left(e^x\right)^{(n)}=e^x & \\
\hline (\sin x)^{(n)}=\sin \left(x+n \frac{\pi}{2}\right) & (n \in \mathbb{N})\\
\hline (\cos x)^{(n)}=\cos \left(x+n \frac{\pi}{2}\right) & (n \in \mathbb{N})\\
\hline \left((1+x)^r\right)^{(n)}=r(r-1) \cdots(r-n+1)(1+x)^{r-n} & (x \gt -1, \quad r \in \mathbb{R})\\
\hline
\end{array}
$$
Aplicaţiile derivatei
Fie $f: D \subset \mathbb{R} \rightarrow \mathbb{R}$ o funcţie şi $a$ un punct al domeniului de definiție $D$.
Punctul $a$ este punct de extrem local pentru $f$ dacă există o vecinătate a sa $V_a$ în care creşterea funcţiei $f(x)-f(a)$ are semn constant; cu alte cuvinte, există $r \gt 0$ a.î.
$$
\text{sgn}(f(x)-f(a))=\text { const. } \quad(\forall) x \in(a-r, a+r) \cap D .
$$
Mai precis,
$a$ este minim local d.d. $\quad f(x)-f(a) \geq 0$,
a este maxim local
d.d. $\quad f(x)-f(a) \leq 0$
$(\forall) x \in(a-r, a+r) \cap D$.
Teorema lui Fermat
Fie $f: D \subset \mathbb{R} \rightarrow \mathbb{R}$ o funcţie şi $a$ un punct din domeniul de definiție $D$.
Dacă $\left \{\begin{array}{l}a \text { este interior lui } D \\ a \text { este punct de extrem local } \\ f \text { este derivabilă în } a\end{array}\right.$, $\quad$ atunci $f^{\prime}(a)=0$.
Interpretarea geometrică
Tangenta la graficul funcţiei într-un punct de extrem local din interiorul domeniului de definiţie al unei funcţii derivabile, este paralelă cu axa $O x$.
Punctul $x_0$ este un punct critic (stationar) al funcţiei derivabile $f$ dacă $f^{\prime}\left(x_0\right)=0$, deci conform teoremei lui Fermat, punctele critice sunt posibile puncte de extrem ale funcţiei.
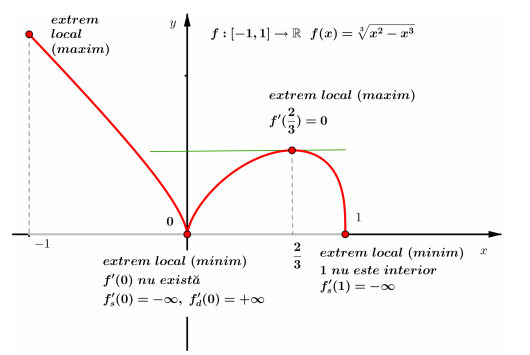
Teorema lui Rolle
Dacă $\left \{\begin{array}{l}f \text { este continuă pe }[a, b] \\ f \text { este derivabilă pe }(a, b) \\ f(a)=f(b)\end{array}\right. , \quad $, atunci $(\exists) c \in(a, b)$ a.î. $f^{\prime}(c)=0$.
În particular, dacă $f(a)=f(b)=0$, teorema afirmă că între două rădăcini ale ecuaţiei $f(x)=0$ există cel puţin o rădăcină a derivatei.
Reciproc, între două rădăcini consecutive ale derivatei, dacă funcţia îşi schimbă semnul, există o singură rădăcină a ecuaţiei $f(x)=0$.
Aplicaţie
Separarea rădăcinilor ecuaţiei $f(x)=0$ cu ajutorul şirului lui Rolle
Dacă $f:(a, b) \rightarrow \mathbb{R}$ este continuă şi derivabilă (extremităţile intervalului pot fi infinite) şi $c_1 \lt c_2 \lt \cdots \lt c_k$ sunt rădăcinile ecuaţiei $f^{\prime}(x)=0$ atunci orice schimbare a semnului în şirul lui Rolle
\begin{array}{c|cccccc}
x & a & c_1 & c_2 & \cdots & c_k & b \\
\hline \text{sgn}(f(x)) & \text{sgn}(f(a)) & \text{sgn}\left(f\left(c_1\right)\right) & \text{sgn}\left(f\left(c_2\right)\right) & & \text{sgn}\left(f\left(x_k\right)\right) & \text{sgn}(f(b))
\end{array}
indică intervalele ce conţin câte o rădăcină a ecuaţiei $f(x)=0$.
Teorema lui Lagrange
$$
\begin{gathered}
\text { Dacă }\left \{\begin{array}{l}
f \text { este continuă pe }[a, b] \\
f \text { este derivabilă pe }(a, b)
\end{array}, \quad \text { atunci }(\exists) c \in(a, b)\right. \text { a.î. } \quad \frac{f(b)-f(a)}{b-a}=f^{\prime}(c)
\end{gathered}
$$
Interpretarea geometrică
Există cel puţin un punct ( $c, f(c)$ ), situat pe graficul funcţiei, în care tangenta este paralelă cu coarda ce uneşte extremităţile $(a, f(a))$ şi $(b, f(b))$.
Consecinţe
Orice funcţie derivabilă pe un interval cu derivata pozitivă (negativă) este crescătoare (descrescătoare) pe acel interval.
Dacă derivata unei funcţii este nulă pe un interval atunci funcţia este constantă pe acel interval:
$$
\begin{gathered}
f: D \subset \mathbb{R} \rightarrow \mathbb{R}, \text { derivabilă pe intervalul } I \subset D \
f^{\prime}(x)=0 \quad(\forall) x \in I \Rightarrow f(x)=c(\text { constantă }) \text { pe } I .
\end{gathered}
$$
Teorema lui Cauchy
$$
\begin{gathered}
\text { Dacă }\left \{\begin{array}{l}
f, g \text { sunt continue pe }[a, b] \\
f, g \text { sunt derivabile pe }(a, b) \text { atunci }(\exists) c \in(a, b) \text { a.î. } \\
g^{\prime}(x) \neq 0 \text { pe }(a, b)
\end{array}\right. \\
\qquad \frac{f(b)-f(a)}{g(b)-f(a)}=\frac{f^{\prime}(c)}{g^{\prime}(c)}
\end{gathered}
$$
Limite de funcţii (completări-regula lui l’Hospital)
Calculul limitelor de funcţii conduce cel mai adesea la situaţii exceptate de la regulile de calcul algebric, cum ar fi $\large \frac{0}{0}$ sau $\large \frac{\infty}{\infty}$, şi este nevoie de multă îndemânare pentru evitarea lor. În condiţii rezonabile de derivabiltate a termenilor, regula lui l’Hospital poate fi de mare ajutor dacă este aplicată corect şi cu discernământ. Pe scurt, regula lui $l^{\prime}$ Hospital reduce calculul limitei $\lim\limits_ {x \rightarrow a} \large \frac{f(x)}{g(x)}$ ( $a$, finit sau infinit) aflată într-una din situaţiile de nedeterminare $\large \frac{0}{0}$ sau $\large \frac{\infty}{\infty}$, la calculul limitei (uneori mai simple) $\lim\limits_ {x \rightarrow a} \large \frac{f^{\prime}(x)}{g^{\prime}(x)}$. Mai precis, dacă $\lim\limits_ {x \rightarrow a} \large \frac{f^{\prime}(x)}{g^{\prime}(x)}=l$ (finit sau infinit) atunci şi $\lim\limits_ {x \rightarrow a} \large \frac{f(x)}{g(x)}=l$.
Exemple
a) $L=\lim\limits _{x \rightarrow 2} \frac{\ln \left(x^2+x-5\right)}{x^2-4}=\frac{0}{0}$, nedeterminare.
Se calculează
$$
\lim\limits_ {x \rightarrow 2} \frac{\left(\ln \left(x^2+x-5\right)\right)^{\prime}}{\left(x^2-4\right)^{\prime}}=\lim\limits_ {x \rightarrow 2} \frac{\frac{2 x+1}{x^2+x-5}}{2 x}=\lim \limits_{x \rightarrow 2} \frac{2 x+1}{2 x\left(x^2+x-5\right)}=\frac{5}{4}
$$
Conform regulii lui $1^{\prime}$ Hospital rezultă $L=\frac{5}{4}$.
b) $L=\lim\limits _{x \rightarrow 0} \frac{x^4+\sin ^2 x^2}{\ln \left(1+\sin ^4 x\right)}=\frac{0}{0}$, nedeterminare.
Limita raportului derivatelor este dificil de calculat
$\lim\limits _{x \rightarrow 0} \frac{\left(\ln \left(x^4+\sin ^2 x^2\right)\right)^{\prime}}{\left(\ln \left(1+\sin ^4 x\right)\right)^{\prime}}=\ldots($ dar nu imposibil de calculat $)$.
Este recomandată metoda directă, bazată pe utilizarea limitelor remarcabile evidenţiate mai sus.
$$
L=\lim\limits_ {x \rightarrow 0} \frac{x^4+\sin ^2 x^2}{\ln \left(1+\sin ^4 x\right)}=\lim\limits_ {x \rightarrow 0} \frac{x^4}{\sin ^4 x} \frac{1+\left(\frac{\sin x^2}{x^2}\right)^2}{\frac{\ln \left(1+\sin ^4 x\right)}{\sin ^4 x}}=1 \cdot \frac{1+1^2}{1}=2 .
$$
c) $L=\lim\limits_ {x \rightarrow 0} \frac{x^2 \sin \frac{1}{x}}{\sin x}=\frac{0}{0}$, nedeterminare. (Am văzut că $\lim\limits_ {x \rightarrow 0} x \sin \frac{1}{x}=0$.) Limita raportului derivatelor nu există $\lim\limits_ {x \rightarrow 0} \frac{\left(x^2 \sin \frac{1}{x}\right)^{\prime}}{(\sin x)^{\prime}}=\lim\limits_ {x \rightarrow 0} \frac{2 x \sin \frac{1}{x}-\sin \frac{1}{x}}{\cos x}$, deoarece $\lim\limits_ {x \rightarrow 0} \sin \frac{1}{x}$ nu există. Totuşi limita există: $L=\lim\limits_ {x \rightarrow 0} \frac{x^2 \sin \frac{1}{x}}{\sin x}=\lim\limits_ {x \rightarrow 0}\left(\frac{x}{\sin x}\right)\left(x \sin \frac{1}{x}\right)=1 \cdot 0=0$. d) $L=\lim\limits_ {x \rightarrow \infty} \frac{x}{\sqrt{x^2+1}}=\frac{\infty}{\infty}$, nedeterminare.
Utilizarea (fără discernământ) a regulii lui l’Hospital nu duce la niciun rezultat: $\lim\limits_ {x \rightarrow \infty} \frac{(x)^{\prime}}{\left(\sqrt{x^2+1}\right)^{\prime}}=\lim\limits_ {x \rightarrow \infty} \frac{\sqrt{x^2+1}}{x}$.
Totuşi limita poate fi calculată cu metoda factorului forţat:
$$
L=\lim\limits_ {x \rightarrow \infty} \frac{x}{\sqrt{x^2+1}}=\lim\limits_ {x \rightarrow \infty} \frac{1}{\sqrt{1+\frac{1}{x^2}}}=1
$$
Ghid pentru reprezentarea grafică a funcţiilor
Etapele reprezentării grafice a funcţiilor reale de variabilă reală $f: E \subset \mathbb{R} \rightarrow \mathbb{R}, \quad f(x)=\ldots$
- Stabilirea domeniului maxim de definiţie $E$
Domeniul maxim de definiţie $E$ este alcătuit din toate numerele reale $x$ pentru care expresia $f(x)$ are sens şi este finită: $E={x \mid f(x) \in \mathbb{R}}$. Mulţimea $E$ este de regulă o reuniune de intervale şi eventual, de puncte “izolate”. - Limitele funcţiei la extremităţile (finite şi infinite) ale intervalelor din $E$
Domeniului de continuitate: $E_c=\{x \mid x \in E$ şi $f$ este continuă în $x\}$ este o reuniune de intervale deschise sau închise.
Asimptote verticale:
$a$, extremitate de interval al domeniului $E_c, a \neq \pm \infty$;
$x=a$ este asimptotă verticală dacă cel puţin una dintre limitele laterale $f(a-0)$ sau $f(a-0)$ este infinită.
Asimptote oblice (sau, în particular, orizontale):
$y=n$ este asimptotă orizontală dacă $\lim\limits_ {x \rightarrow-\infty} f(x)=n$ sau $\lim\limits_ {x \rightarrow \infty} f(x)=n$;
$y=m x+n$ este asimptotă oblică dacă $\lim\limits_ {x \rightarrow \pm \infty} f(x)$ este infinită sau nu există, dar $m=\lim\limits_ {x \rightarrow \pm \infty} \frac{f(x)}{x}$ şi $n=\lim\limits _{x \rightarrow \pm \infty}(f(x)-m x)$ există şi sunt finite. - Studiul derivatei întâi
Calculul derivatei întâi $f^{\prime}(x)$.
Domeniului de derivabilitate este domeniul maxim de existenţă al expresiei $f^{\prime}(x): E_d=\left \{x \mid x \in E_c\right.$ şi $f$ este derivabilă în $\left.x\right \}$.
Practic, pentru precizarea domeniului $E_d$, se calculează derivatele laterale $f_s^{\prime}(b)$ şi $f_d^{\prime}(b)$ în acele puncte $b$ ale domeniului de continuitate $E_c$ în care există dubii asupra existenţei expresiei $f^{\prime}(x)$.- Dacă $f_s^{\prime}(b)$ şi $f_d^{\prime}(b)$ sunt finite şi egale atunci $b$ aparţine domeniului de derivabilitate $E_d$.
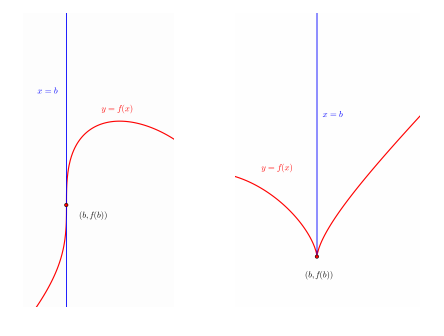
- Dacă $f_s^{\prime}(b)$ şi $f_d^{\prime}(b)$ sunt infinite, egale atunci $f$ nu este derivabilă în $b$, (b, $f(b)$ ) este un punct de inflexiune cu tangentă verticală al graficului iar dreapta $x=b$ este tangentă verticală.
- Dacă $f_s^{\prime}(b)$ şi $f_d^{\prime}(b)$ sunt infinite, diferite atunci $f$ nu este derivabilă în $b$, ( $b, f(b)$ ) este un punct de intoarcere al graficului iar semidreapta $x=b$ (cu $y \geq f(b)$ sau cu $y \leq f(b)$, după caz) este semitangentă verticală.
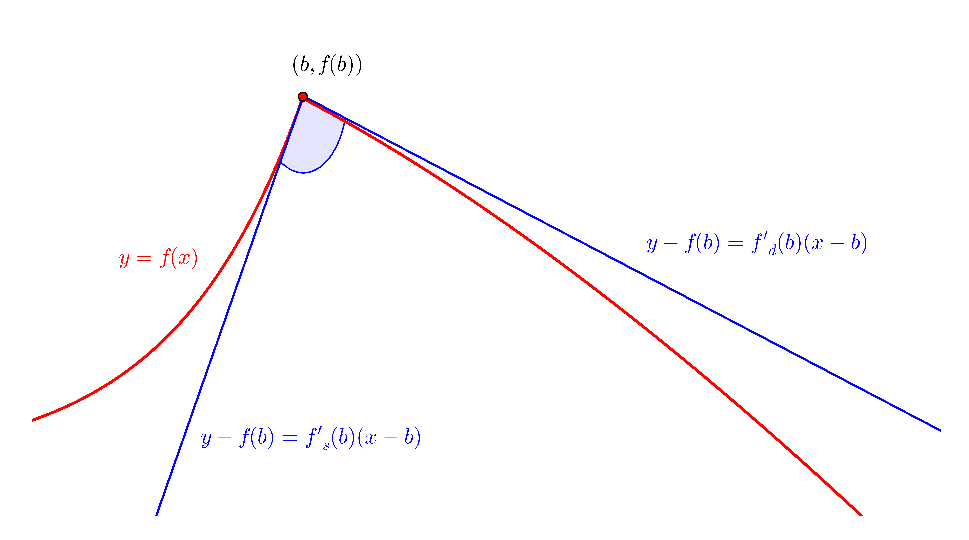
- Dacă $f_s^{\prime}(b)$ şi $f_d^{\prime}(b)$ sunt finite şi diferite sau cel puţin una dintre derivatele laterale este finită atunci funcţia nu este derivabilă în $b,(b, f(b))$ este un punct unghiular al graficului.
Se rezolvă ecuaţia $f^{\prime}(x)=0$. Rădăcinile derivatei sunt punctele critice sau staţionare ale funcţiei.
Importanţa studiului amănunţit al derivatei întâi constă în următoarele:
-punctele de extrem ale funcţiei se găsesc printre punctele sale critice, unghiulare sau de întoarcere;
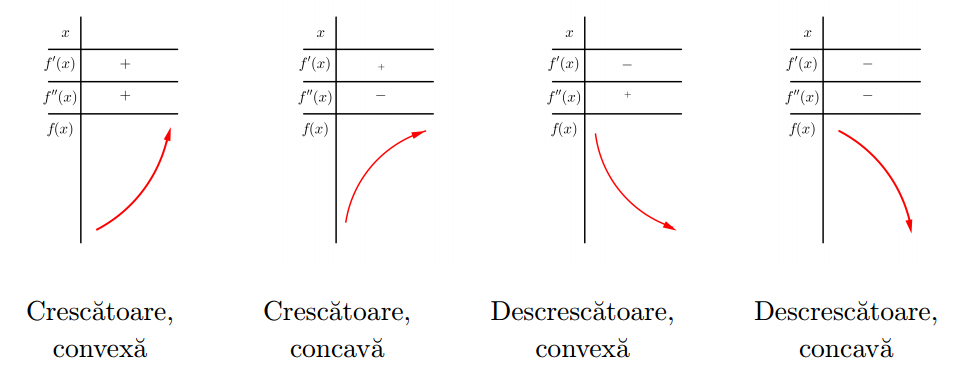
-semnul derivatei întâi oferă informaţii despre intervalele de monotonie: $f^{\prime}(x) \geq 0$ pe intervalul $I \subset E_d \Rightarrow f$ este crescătoare pe $I$, $f^{\prime}(x) \leq 0$ pe intervalul $I \subset E_d \Rightarrow f$ este descrescătoare pe $I$.
- Dacă $f_s^{\prime}(b)$ şi $f_d^{\prime}(b)$ sunt finite şi egale atunci $b$ aparţine domeniului de derivabilitate $E_d$.
- Studiul derivatei a doua
Calculul derivatei a doua $f^{\prime \prime}(x)$
Precizarea domeniului maxim de existenţă al expresiei $f^{\prime \prime}(x)$
Se determină rădăcinile ecuaţiei $f^{\prime \prime}(x)=0$
Punctele de inflexiune ale funcţiei se găsesc printre rădăcinile derivatei a doua. Semnul derivatei a doua stabileşte intervalele pe care funcţia este concavă sau convexă
$f^{\prime \prime}(x) \geq 0$ pe intervalul $I \Rightarrow f$ este convexă pe $I$
$f^{\prime \prime}(x) \leq 0$ pe intervalul $I \Rightarrow f$ este concavă pe $I$
Dacă expresia $f^{\prime}(x)$ are o formă complicată (calculul lui $f^{\prime \prime}(x)$ ia mult timp) sau ecuaţia $f^{\prime \prime}(x)=0$ este dificil de rezolvat, se poate renunţa la studiul derivatei a doua. - Tabelul de variatie al functiei
$$
\begin{aligned}
&\text { Tabelul de variatie al functiei }\\
&\begin{array}{c||l}
x & \text { Se aşază crescător punctele importante determinate mai sus. } \\
\hline \hline f^{\prime}(x) & \text { Se studiază semnul pe fiecare interval evidenţiat la rubrica } x . \\
\hline f^{\prime \prime}(x) & \text { Se studiază semnul pe fiecare interval evidenţiat la rubrica } x . \\
\hline f(x) & \begin{array}{l}
\text { Pe fiecare interval se trasează săgeţile ce indică monotonia } \\
\text { şi forma ramurilor ce alcătuiesc graficul funcţiei, } \\
\text { respectând următoarele reguli: }
\end{array}
\end{array}
\end{aligned}
$$
- Valori importante
Se calculează coordonatele punctelor în care funcţia nu este continuă, nu este derivabilă, ale punctelor critice şi ale punctelor de inflexiune. Valorile găsite se trec în tabelul de variaţie al funcţiei.
Se calculează coordonatele punctelor de intersecţie cu axele:
$$
\begin{array}{ll}
\cap O x & y=0 \Leftrightarrow f(x)=0 \quad(\text { se reţin doar valorile } x \in E) . \\
\cap O y & x=0 \Rightarrow y=f(0) \quad(\text { doar dacă } 0 \in E) .
\end{array}
$$ - Reprezentarea grafică
-se trasează axele de coordonate,
-se stabileşte unitatea de măsură pe fiecare axă în parte,
-se trasează asimptotele şi tangentele verticale,
-se aşează pe grafic punctele importante ale căror coordonate au fost calculate mai sus,
-se trasează graficul funcţiei conform tabelului de variaţie. - Observaţii
Se studiază eventualele simetrii ale graficului.
Dacă $f$ este o funcţie pară, adică $f(-x)=f(x)(\forall) x \in E$, atunci graficul funcţiei este simetric faţă de axa $O y$.
Dacă $f$ este o funcţie impară, adică $f(-x)=-f(x)(\forall) x \in E$, atunci graficul funcţiei este simetric faţă de origine.
Se studiază periodicitatea.
Funcţia $f$ este periodică cu perioada $T$ dacă $f(x+T)=f(x)(\forall) x \in E$; cel mai mic număr pozitiv $T$ cu această proprietate (dacă există) se numeşte perioada principală.
Se precizează imaginea funcţiei: $\text{Im} f= \{y \mid(\exists) x \in E$ a.î. $y=f(x) \}$.
Integrabilitate şi aplicaţii
Definiţie
Funcţia $f: D \rightarrow \mathbb{R}(D \subset \mathbb{R}$, interval) este primitivabilă dacă există o funcţie $F: D \rightarrow \mathbb{R}$, numită primitiva lui $f$, având proprietăţile:
(i) $F$ este derivabilă pe $D$
(ii) $F^{\prime}(x)=f(x),(\forall) x \in D$.
Mulţimea tuturor primitivelor lui $f$ este notată prin simbolul “$\displaystyle\int f(x) d x$ ” ce se citeşte “integrala nedefinită a lui $f$ in raport cu $x$ “. Întrucât orice două primitive ale aceleaşi funcţii primitivabile diferă printr-o constantă ( $f$ este definită pe un interval!), pentru determinarea integralei nedefinite este suficientă găsirea unei singure primitive $F$. Are loc egalitatea de mulțimi
$$
\int f(x) d x=F(x)+\text{C}
$$
unde $\text{C}$ reprezintă mulțimea funcţiilor reale constante definite pe $D$.
Proprietatea (ii) din definiție permite alcătuirea unui tabel cu integrale nedefinite a cărui consultare atentă reprezintă o primă metodă de primitivare. În plus, din (ii) rezultă şi proprietatea de liniaritate a integralei nedefinite:
$$
\displaystyle\int [\alpha f(x)+\beta g(x)] d x=\alpha \int f(x) d x+\beta \int g(x) d x
$$
oricare ar fi $f, g: D \rightarrow \mathbb{R}$, primitivabile şi $\alpha, \beta$ numere reale.
$$
\begin{aligned}
&\text { Tabelul primitivelor elementare } \\
&\begin{gathered}
\int x^n d x=\frac{x^{n+1}}{n+1}+\text{C}, \quad x \in I \subset \mathbb{R}, n \in \mathbb{N} \\
\int x^r d x=\frac{x^{r+1}}{r+1}+\text{C}, \quad x \in I \subset \mathbb{R}{+}^, \quad r \in \mathbb{R} \backslash{-1} \\ \int \frac{1}{\sqrt{x}} d x=2 \sqrt{x}+\text{C}, \quad \int \sqrt{x} d x=\frac{2}{3} x \sqrt{x}+\text{C}, \quad x \in I \subset(0, \infty) \\ \int \frac{1}{x} d x=\ln x+\text{C}, \quad x \in I \subset \mathbb{R}{+}^{*} \\
\int a^x d x=\frac{a^x}{\ln a}+\text{C}, \quad x \in I \subset \mathbb{R} \\
\int \frac{1}{x^2+a^2} d x=\frac{1}{a} \text{arctg} \frac{x}{a}+\text{C}, \quad x \in I \subset \mathbb{R} \\
\int \frac{1}{x^2-a^2} d x=\frac{1}{2 a} \ln \left|\frac{x-a}{x+a}\right|+\text{C,} \quad x \in I \subset \mathbb{R} \backslash{-a, a} \\
\int \sin x d x=-\cos x+\text{C}, \quad \int \cos x d x=\sin x+\text{C}, \quad x \in I \subset \mathbb{R} \\
\int \text{tg} x d x=-\ln |\cos x|+\text{C}, \quad x \in I \subset \mathbb{R} \backslash\left \{\left.(2 k+1) \frac{\pi}{2} \right\rvert\, k \in \mathbb{R}\right \} \\
\int \frac{1}{\sin ^2 x} d x=-\text{ctg} x+\text{C}, \quad x \in I \subset \mathbb{R} \backslash{k \pi \mid k \in \mathbb{R}} \\
\int \frac{1}{\cos ^2 x} d x=\text{tg} x+\text{C}, \quad x \in I \subset \mathbb{R} \backslash\left \{\left.(2 k+1) \frac{\pi}{2} \right\rvert\, k \in \mathbb{R}\right \} \\
\int \frac{1}{\sqrt{x^2+a^2}} d x=\ln \left(x+\sqrt{x^2+a^2}\right)+\text{C}, \quad x \in I \subset \mathbb{R} \\
\int \frac{1}{\sqrt{x^2-a^2}} d x=\ln \left|x+\sqrt{x^2-a^2}\right|+\text{C}, \quad x \in I \subset(-\infty,-a) \cup(a,+\infty) \\
\int \frac{1}{\sqrt{a^2-x^2}} d x=\arcsin \frac{x}{a}+\text{C}, \quad x \in I \subset(-a, a)
\end{gathered}
\end{aligned}
$$
În practică îşi dovedesc utilitatea şi următoarele trei formule de integrare ce se pot verifica imediat prin derivarea membrului drept:
$$
\begin{gathered}
\int \frac{x}{\sqrt{x^2+a^2}} d x=\sqrt{x^2+a^2}+\text{C}; \quad \int \frac{x}{\sqrt{x^2-a^2}} d x=\sqrt{x^2-a^2}+\text{C} \\
\int \frac{x}{\sqrt{a^2-x^2}} d x=-\sqrt{a^2-x^2}+\text{C}
\end{gathered}
$$
Problema A
Cum se poate decide dacă funcţia $f: D \rightarrow \mathbb{R}(D \subset \mathbb{R}$, interval) este sau nu primitivabilă?
Direct, problema poate fi rezolvată intuind (de exemplu cu ajutorul tabelului) forma pe care ar trebui s-o aibă primitiva $F$ şi verificând dacă sunt sau nu îndeplinite condiţiile (i) şi (ii) din definiţie.
Posibilitatea rezolvării indirecte a problemei A se bazează pe următoarele rezultate:
- Orice funcţie reală continuă pe intervalul $D \subset \mathbb{R}$ este primitivabilă pe $D$.
- Dacă $f$ este o funcţie reală primitivabilă pe intervalul $D \subset \mathbb{R}$ atunci din identitatea $f=F^{\prime}$ rezultă imediat că $f$ are proprietatea lui Darboux pe $D$.
i) Dacă $f$ nu are proprietatea lui Darboux pe intervalul $D$ atunci $f$ nu este primitivabilă pe $D$.
ii) Dacă $f$ are in punctul $x_0$ al intervalului $D$ o discontinuitate de speţa I (adică limitele laterale $f\left(x_0-0\right)$ şi $f\left(x_0+0\right)$ sunt finite dar diferite) atunci $f$ nu este primitivabilă pe $D$.
Astfel, pentru a dovedi primitivabilitatea unei funcţii este suficient (nu şi necesar) să se verifice continuitatea sa, ceea ce este mult mai comod în comparaţie cu verificarea condiţiilor i) şi ii) ale definiţiei.
Pentru a dovedi neprimitivabilitatea unei funcţii este suficient (nu şi necesar) să se verifice că $f$ nu posedă proprietatea lui Darboux, adică faptul că există un interval $D_0 \subset D$ a cărui imagine prin $f$,
$f\left(D_0\right)=\left \{y \mid y \in \mathbb{R},(\exists) x_0 \in D_0: y=f\left(x_0\right)\right \}$ nu este interval.
Problema B
Cum poate fi determinată integrala nedefinită $\mathcal{I}=\displaystyle\int f(x) d x$ a funcţiei primitivabile $f: D \rightarrow \mathbb{R}(D \subset \mathbb{R}$, interval $)$ ?
O primă metodă o constituie, aşa cum remarcam înainte, consultarea atentă a tabelului cu primitivele unor funcţii elementare. Descriem în continuare câreva procedee de calcul a integralei nedefinite utile în rezolvarea problemelor.
METODA INTEGRĂRII PRIN PĂRŢI
Dacă $f$ se poate exprima sub forma
$$
f(x)=u(x) \cdot v^{\prime}(x)
$$
cu $u, v: D \rightarrow \mathbb{R}$ derivabile, atunci
$$
\mathcal{I}=\int f(x) d x=u(x) \cdot v(x)-\int u^{\prime}(x) \cdot v(x) d x=\ldots=F(x)+C
$$
(cu alte cuvinte, calculul integralei inițiale $\int u(x) \cdot v^{\prime}(x) d x$ se reduce la cel al integralei $\int u^{\prime}(x) \cdot v(x) d x$ care, la o alegere judicioasă a funcţiilor $u$ şi $v$, poate fi mai simplă).
METODA SCHIMBĂRII DE VARIABILĂ (1)
Dacă $f$ se poate exprima sub forma:
$$
f(x)=g(\varphi(x)) \cdot \varphi^{\prime}(x)
$$
unde $\varphi: D \rightarrow E(E \subseteq \mathbb{R}$ interval) este derivabilă iar $f: E \rightarrow \mathbb{R}$ este primitivabilă cu primitiva $G$, atunci calculul integralei nedefinite
$$
\mathcal{I}=\int f(x) d x=\int g(\varphi(x)) \cdot \varphi^{\prime}(x) d x
$$
prin schimbarea de variabilă $t=\varphi(x)$, se reduce la calculul integralei nedefinite:
$$
\mathcal{I}_t=\int g(t) d t=\ldots=G(t)+C
$$
şi în final
$$
\mathcal{I}=G(\varphi(x))+C
$$
METODA SCHIMBĂRII DE VARIABILĂ (2)
Dacă $\Psi: E \rightarrow \mathbb{R}\left(E \subseteq \mathbb{R}\right.$, interval) este bijectivă şi derivabilă iar $(f \circ \Psi) \cdot \Psi^{\prime}$ este primitivabilă pe $E$ cu primitiva $H$ atunci calculul integralei nedefinite
$$
\mathcal{I}=\int f(x) d x
$$
se reduce prin schimbarea de variabilă (substituţia) $x=\Psi(t)$ la cel al integralei
$$
\mathcal{I}_t=\int f(\Psi(t)) \cdot \Psi^{\prime}(t) d t=\ldots=H(t)+C
$$
iar în final, revenind la variabila iniţială (în baza bijectivităţii lui $\Psi$, $t=\Psi^{-1}(x)$ ), se obţine:
$$
\mathcal{I}=H\left(\Psi^{-1}(x)\right)+C
$$
SUBSTITUŢII REMARCABILE
Utilizarea formei canonice a trinomului de gradul al-II-lea
$$
\begin{gathered}
a x^2+b x+c=\frac{4 a}{4 a}\left(a x^2+b x+c\right)=\frac{1}{4 a}\left(4 a^2 x^2+4 a b x+4 a c\right)= \\
=\frac{1}{4 a}\left[(2 a x+b)^2+\Delta\right] \\
\mathcal{I}_x=\int f\left(a x^2+b x+c\right) d x \quad \text { cu } f \text { integrabilă } \\
t=2 a x+b \Rightarrow \mathcal{I}_t=\frac{1}{2 a} \int g(t) d t, \quad \text { unde } \quad g(t)=f\left(\frac{t^2+\Delta}{4 a}\right)
\end{gathered}
$$
Primitivarea functiilor raţionale
$$
\begin{aligned}
& \mathcal{I}=\int R(x) d x=\int \frac{P(x)}{Q(x)} d x \\
& \qquad \begin{array}{l}
g r P \geq g r Q \Rightarrow R=C+\frac{\rho}{Q}(\rho, \text { restul }) \Rightarrow \mathcal{I}=\int C(x) d x+\int \frac{\rho(x)}{Q(x)} d x \\
g r P \lt g r Q \Rightarrow Q \quad \begin{array}{l}
\text { se descompune în produs de factori } \\
\text { de gr.I şi II la diverse puteri }
\end{array} \\
R=\frac{P}{Q} \text { se descompune în fracţii simple de forma } \\
\frac{A}{(a x+b)^n} \text { respectiv } \frac{A x+B}{\left(a x^2+b x+c\right)^m}(c u \Delta \lt 0)
\end{array}
\end{aligned}
$$
Substituţii trigonometrice pentru eliminarea radicalului
$$
\begin{array}{ll}
\displaystyle\int f\left(\sqrt{a^2-x^2}\right) d x & x=a \cdot \sin t \\
\displaystyle\int f\left(\sqrt{x^2+a^2}\right) d x & x=a \cdot \operatorname{tg} t \\
\displaystyle\int f\left(\sqrt{x^2-a^2}\right) d x & x=\frac{a}{\cos t}
\end{array}
$$
Substituţiile lui Euler
$$
\begin{aligned}
& \int R\left(x, \sqrt{a x^2+b x+c}\right) d x \quad \text { cu } R, \text { raţională } \\
& \left \{\begin{array}{l}
\Delta \lt 0 \Rightarrow t \pm \sqrt{a} x=\sqrt{a x^2+b x+c} \\ \Delta \gt 0 \Rightarrow t=\sqrt{a \frac{x-x_1}{x-x_2}}
\end{array}\right.
\end{aligned}
$$
Integrale reductibile la integrale de funcţii raţionale
$$
\begin{array}{r}
\displaystyle\int R\left(x, \sqrt[p]{\frac{a x+b}{c x+d}}, \ldots, \sqrt[q]{\frac{a x+b}{c x+d}}\right) d x \quad R, \text { raţională } \\
t=\sqrt[m]{\frac{a x+b}{c x+d}},\text { unde } m=[p, . ., q]
\end{array}
$$
reprezintă cel mai mic multiplu comun al numerelor $p, \ldots, q$.
$$
\displaystyle\int R\left(e^x\right) d x \quad R, \text { raţională } \quad t=e^x
$$
$$
\int R(\cos x, \sin x) d x \quad R, \text { raţională } \begin{cases} & t=\operatorname{tg} \frac{x}{2} \\ R(u,-v)=-R(u, v) \Rightarrow & t=\cos x \\ R(-u, v)=-R(u, v) \Rightarrow & t=\sin x \\ R(-u,-v)=R(u, v) \Rightarrow & t=\operatorname{tg} x\end{cases}
$$
Precizăm în încheiere că alegerea schimbării de variabilă ţine de imaginaţia şi experienţa rezolvitorului care poate aborda o aceeaşi problemă prin două sau chiar mai multe modalităţi. Este interesant să comparaţi în asemenea situaţii rezultatele obţinute şi să explicaţi diferenţele remarcate. De asemenea este util ca la integralele nedefinite întâlnite să reflectaţi asupra intervalelor maxime pe care sunt definite funcţiile de sub semnul integralei.
Construcţia integralei definite
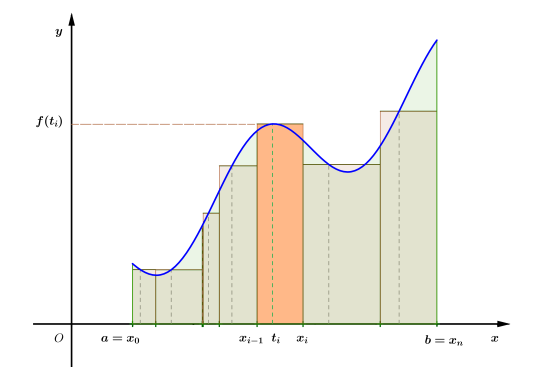
Oricărei funcţii $f:[a, b] \rightarrow \mathbb{R}$ i se poate ataşa un număr real $\sigma_f$ după cum urmează:
- se construieşte o diviziune a intervalului de definiţie:
( $\Delta$ ) $\quad a=x_0 \lt x_1 \lt x_2 \lt \ldots \lt x_{i-1} \lt x_i \lt \ldots \lt x_{n-1} \lt x_n=b$, - se alege un sistem de puncte intermediare diviziunii:
$(\tau)\left \{t_1, t_2, \ldots, t_i, \ldots, t_n\right \}, \quad t_i \in\left[x_{i-1}, x_i\right] \quad(i=\overline{1, n})$, - se defineşte
$$
\sigma_f(\Delta, \tau)=\sum_{i=1}^n f\left(t_i\right)\left(x_i-x_{i-1}\right) .
$$
Numărul $\sigma_f(\Delta, \tau)$ se numeşte suma integrală Riemann a lui $f$ relativ la diviziunea $(\Delta)$ şi sistemul de puncte intermediare $(\tau)$. Din punct de vedere geometric, pentru funcţii pozitive, acest număr reprezintă o aproximare a ariei “de sub grafic”.
Definiţie
Funcţia $f:[a, b] \rightarrow \mathbb{R}$ este integrabilă (în sens Riemann) d.d. există un număr real $\mathbb{I}$ care verifică următoarea proprietate:
“pentru orice număr $\varepsilon \gt 0$ există $\delta_{\varepsilon} \gt 0$ aşa încât oricare ar fi diviziunea $(\Delta)$ cu norma $\mu(\Delta):=\max i\left(x_i-x{i-1}\right) \lt \delta_{\varepsilon} \quad$ şi oricare ar fi sistemul de puncte ( $\tau$ ), intermediare diviziunii ( $\Delta$ ), are loc inegalitatea $\left|\sigma_f(\Delta, \tau)-\text{I}\right| \lt \varepsilon$ “.
Numărul $\text{I}$, dacă există, se notează $\displaystyle\int_a^b f(x) d x$ şi reprezintă “integrala definită a funcţiei $f$ pe intervalul $[a, b]$ in raport cu variabila $x$ “.
În cazul particular al partiţiei uniforme cu noma $\frac{b-a}{n}$ rezultă
$$
\lim\limits_ {n \rightarrow \infty} \frac{1}{n} \sum\limits_{k=1}^n f\left(a+\frac{k(b-a)}{n}\right)=\displaystyle\int_a^b f(x) d x
$$
Problema C
Cum se poate decide dacă funcţia $f:[a, b] \rightarrow \mathbb{R}$ este sau nu integrabilă?
Utilizarea definiţiei, deşi incomodă, este uneori inevitabilă.
Următoarele rezultate sunt utile pentru evitarea definiţiei în studiul integrabilităţii:
- Oricare funcţie integrabilă pe $[a, b]$ este mărginită pe $[a, b]$.
- Funcţiile reale nemărginite nu sunt integrabile.
- Orice funcţie reală monotonă pe $[a, b]$ este integrabilă pe $[a, b]$.
- Dacă $f:[a, b] \rightarrow \mathbb{R}$ este continuă pe $[a, b] \backslash\left \{x_1, x_2, \ldots, x_k\right \}$ iar punctele de discontinuitate $x_i(i=\overline{1, k})$ sunt toate de speţa întâi $\left(f\left(x_i-0\right)\right.$ şi $f\left(x_i+0\right)$ există, sunt finite dar diferite) atunci $f$ este integrabilă pe $[a, b]$.
Problema D
Cum poate fi calculată integrala definită $\mathcal{I}=\int_a^b f(x) d x$ ?
Pentru a calcula integralele este bine să cunoaşteţi:
a) Proprietatea de liniaritate:
$$
\displaystyle\int_a^b[\alpha f(x)+\beta g(x)] d x=\alpha \displaystyle\int_a^b f(x) d x+\beta \displaystyle\int_a^b g(x) d x, \quad \alpha, \beta \in \mathbb{R}
$$
b) Proprietatea de aditivitate la interval:
$$
\displaystyle\int_a^b f(x) d x=\displaystyle\int_a^c f(x) d x+\displaystyle\int_c^b f(x) d x
$$
$g$ integrabilă iar $c \in[a, b]$.
FORMULA LUI LEIBNIZ-NEWTON
Dacă funcţia $f:[a, b] \rightarrow \mathbb{R}$ este integrablă şi primitivabilă iar $F$ este o primitivă a sa atunci
$$
\displaystyle\int_a^b f(x) d x=F(b)-F(a)
$$
Există funcţii integrabile care nu sunt primitivabile ceea ce face ca formula să nu poată fi aplicată. Un caz aparte, în care nu se poate utiliza (direct) formula este acela al integralei unei funcţii, integrabile si primitivabile, a cărei primitivă nu este exprimabilă prin funcţii elementare. Asemenea funcţii sunt $e^{-x^2}, \cos x^2, \large \frac{\sin x}{x}$.
METODE DE INTEGRARE
Integrarea prin părţi se aplică dacă $f(x)=u(x) \cdot v^{\prime}(x)$
$$
\displaystyle\int_a^b f(x) d x=\displaystyle\int_a^b u(x) \cdot v^{\prime}(x) d x=\left.u(x) \cdot v(x)\right|_a ^b-\displaystyle\int_a^b u^{\prime}(x) \cdot v(x) d x=\ldots
$$
Schimbarea de variabilă (1) se aplică dacă $f(x)=g(\varphi(x)) \cdot \varphi^{\prime}(x)$
$$
\begin{aligned}
& \mathcal{I}=\displaystyle\int_a^b f(x) d x=\displaystyle\int_a^b g(\varphi(x)) \cdot \varphi^{\prime}(x) d x \\
& t=\varphi(x) \Rightarrow d t=\varphi^{\prime}(x) d x \\
& x=a \Rightarrow t=\varphi(a) \text { şi } x=b \Rightarrow t=\varphi(b) \\
& \mathcal{I}=\displaystyle\int_{\varphi(a)}^{\varphi(b)} g(t) d t=G(\varphi(b))-G(\varphi(a))
\end{aligned}
$$
Schimbarea de variabilă (2) se aplică dacă $f(x)$ are o formă specială (vezi lista substituţiilor remarcabile)
$$
\begin{aligned}
& \mathcal{I}=\displaystyle\int_a^b f(x) d x \\
& t=\varphi(x) \Leftrightarrow x=\psi(t) \quad\left(\psi=\varphi^{-1}\right) \\
& x=\psi(t) \Rightarrow d x=\psi^{\prime}(t) d t \\
& x=a \Rightarrow t=\varphi(a) \quad \text { şi } \quad x=b \Rightarrow t=\varphi(b) \\
& \mathcal{I}=\displaystyle\int_{\varphi(a)}^{\varphi(b)} f(\psi(t)) \cdot \psi^{\prime}(t) d t=H(\varphi(b))-H(\varphi(a))
\end{aligned}
$$
Proprietăţile integralei definite
Teoremă
Dacă funcţia $f:[a, b] \rightarrow \mathbb{R}$ este continuă atunci
i) $f$ este integrabilă pe $[a, b]$,
ii) $f$ este primitivabilă pe $[a, b]$ iar $F:[a, b] \rightarrow \mathbb{R}, F(x)=\displaystyle\int_a^x f(t) d t$ este o primitivă a lui $f$.
Pentru orice funcţie continuă $f:[a, b] \rightarrow \mathbb{R}$ are loc identitatea
$$
\frac{d}{d x}\left(\displaystyle\int_a^x f(t) d t\right)=f(x)
$$
Observaţie
Integrarea şi derivarea sunt operaţii “inverse” una celeilalte în sensul că
$$
\displaystyle\int g^{\prime}(x) d x=g(x)+\mathcal{C} \quad \text { şi } \quad\left(\displaystyle\int_a^x g(t) d t\right)_x^{\prime}=g(x)
$$
Теоrеmӑ
Dacă $f, g:[a, b] \rightarrow \mathbb{R}$ sunt integrabile atunci
$$
f(x) \leq g(x), \quad(\forall) x \in[a, b] \Rightarrow \displaystyle\int_a^b f(x) d x \leq \displaystyle\int_a^b g(x) d x
$$
Теоrеmӑ
Dacă $f:[a, b] \rightarrow \mathbb{R}$ este integrabilă şi $m=\inf \limits_{x \in[a, b]} f(x),$ respectiv $M=$ $\sup\limits_ {x \in[a, b]} f(x),$ atunci
$$
m(b-a) \leq \displaystyle\int_a^b f(x) d x \leq M(b-a)
$$
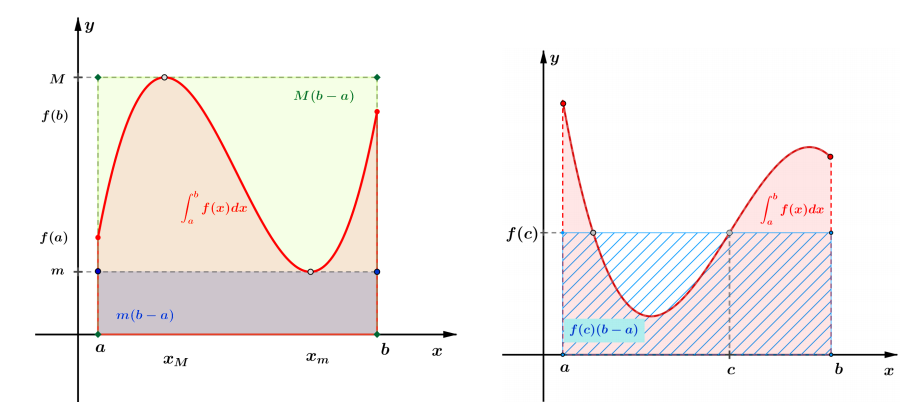
Teoremă (formula de medie)
Dacă $f:[a, b] \rightarrow \mathbb{R}$ este integrabilă atunci există un punct $c$ situat între $a$ şi $b$ aşa încât
$$
\int_a^b f(x) d x=f(c)(b-a)
$$
Numărul $\frac{1}{b-a} \displaystyle\int_a^b f(x) d x$ se numeşte valoarea medie a funcţiei $f$ pe intervalul $[a, b]$.
Aplicaţii ale integralei definite in geometrie
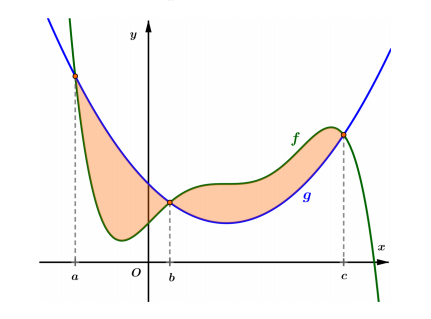
i) Aria domeniilor mărginite cuprinse între graficele a două funcţii
Dacă $f, g: I \subseteq \mathbb{R} \rightarrow \mathbb{R}$ două funcţii continue ale căror grafice se intersectează în punctele de abscise $a \lt b \lt c$ determină un domeniu mărginit a cărui arie este
$$
A_{f, g}=\displaystyle\int_a^c|g(x)-f(x)| d x
$$
Exemplu
Aria discului circular de rază $r$ (centrat în origine)
$$
D=\left \{(x, y) \mid x^2+y^2 \leq r^2\right \}=\left \{(x, y) \mid-\sqrt{r^2-x^2} \leq y \leq \sqrt{r^2-x^2}\right \}
$$
$$
\begin{aligned}
\text{Aria}(D) & =\displaystyle\int_{-r}^r\left|\sqrt{r^2-x^2}-\left(-\sqrt{r^2-x^2}\right)\right| d x=2 \displaystyle\int_{-r}^r \sqrt{r^2-x^2} d x= \\
& =4 \displaystyle\int_0^r \sqrt{r^2-x^2} d x=\left|2 r^2 \arcsin \frac{x}{r}+2 x \sqrt{r^2-x^2}\right|_0^r=r^2 \pi
\end{aligned}
$$
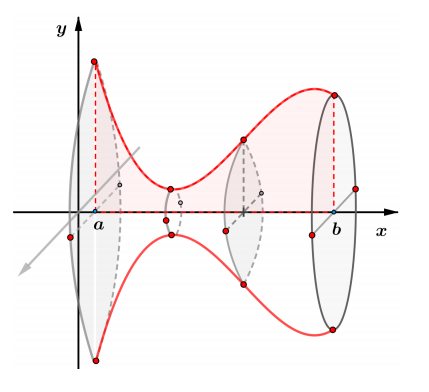
ii) Volumul corpurilor generate prin rotirea graficului functiei in jurul axei $O x$
Dacă $f: I \subseteq \mathbb{R} \rightarrow \mathbb{R}$ o funcţie continuă atunci corpul generat prin rotirea porţiunii de grafic cuprinsă între punctele $x=a$ şi $x=b$ în jurul axei $O x$ are volumul
$$
V_f=\pi \displaystyle\int_a^b f^2(x) d x
$$