Cuprins
Aplicaţiile trigonometriei în geometrie
Numere complexe (Aplicații ale numerelor complexe în algebră)
Elemente de geometrie analitică
Funcţiile trigonometrice
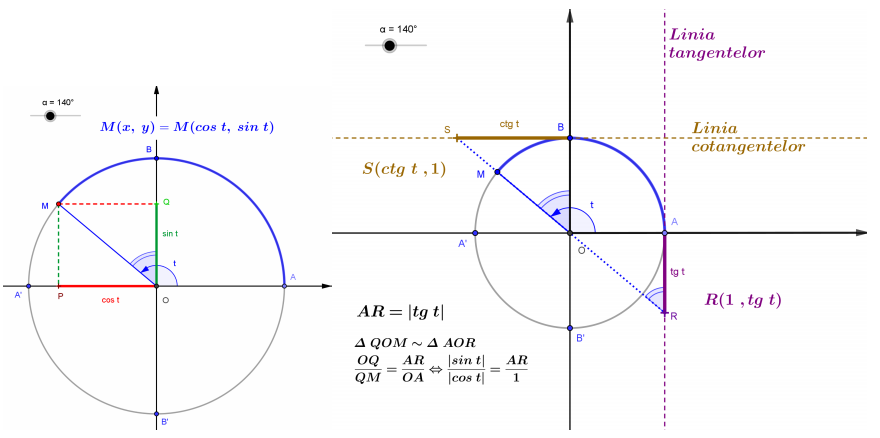
$\mathcal{C}(O ; 1)=\left \{(x, y) \mid x^2+y^2=1\right \}$-cercul trigonometric (centrat în originea axelor de coordonate curaza 1 ).
$M(x, y)$-punctul curent pe cercul trigonometric.
$t \in[0,2 \pi)$-măsura în radiani a unghiului la centru format de semiaxa $O x_{+}$ cu raza vectoare $O M$.
Corespondenţa $t \longleftrightarrow M(x, y)$ este bijectivă .

Definiţii $\quad \cos t=x, \quad \sin t=y, \quad \operatorname{tg} t=\frac{y}{x} \quad$ şi $\quad \operatorname{ctg} t=\frac{x}{y}$.
Definiţia se poate extinde de la intervalul $[0,2 \pi)$ la $\mathbb{R}$ prin procedeul numit ” reducerea la perioada principală”:
$$
\begin{gathered}
(\forall) t \in \mathbb{R} \quad(\exists!) t^* \in[0,2 \pi) \text { a.î. } t=t^{*}+2 k \pi, \text { unde } k \in \mathbb{Z}, k=\left[\frac{t}{2 \pi}\right] \ t \in \mathbb{R} \Rightarrow \quad \cos t=\cos t^* \text { şi } \sin t=\sin t^*
\end{gathered}
$$
Proprietăţile funcţiilor cos şi sin
$\cos$ şi $\sin$ sunt mărginite: $\quad|\cos t| \leq 1$ şi $|\sin t| \leq 1 \quad(\forall) t \in \mathbb{R}$. cos şi sin sunt periodice cu perioada $2 \pi: \begin{array}{ll}\cos (t+2 k \pi)=\cos t & (\forall) t \in \mathbb{R} \ \sin (t+2 k \pi)=\sin t & (\forall) k \in \mathbb{Z}\end{array}$
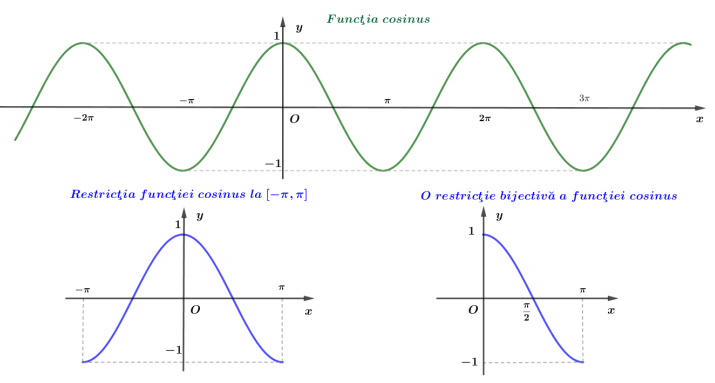
$\cos : \mathbb{R} \rightarrow[-1,1]$ este o funcţie pară, adică $\cos (-t)=\cos t$.
Funcţia cos este pozitivă în cadranele I şi IV, resp. negativă în II şi III.
$\sin : \mathbb{R} \rightarrow[-1,1]$ este o funcţie impară, adică $\sin (-t)=-\sin t$.
Funcţia sin este pozitivă în cadranele $I$ şi $I I$ resp. negativă în $I I I$ şi $I V$.
$$
\begin{aligned}
&\text { Tabelul de valori al funcţiilor sin şi cos }\\
&\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline o & 0 & 30 & 45 & 60 & 90 & 120 & 135 & 150 & 180 \\
\hline \mathrm{rad} & 0 & \frac{\pi}{6} & \frac{\pi}{4} & \frac{\pi}{3} & \frac{\pi}{2} & \frac{2 \pi}{3} & \frac{3 \pi}{4} & \frac{5 \pi}{6} & \pi \\
\hline \sin & 0 & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & 0 \\
\hline \cos & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & 0 & -\frac{1}{2} & -\frac{\sqrt{2}}{2} & -\frac{\sqrt{3}}{2} & -1 \\
\hline
\end{array}
\end{aligned}
$$
$$
\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline o & 180 & 210 & 225 & 240 & 270 & 300 & 315 & 330 & 360 \\
\hline \mathrm{rad} & \pi & \frac{7 \pi}{6} & \frac{5 \pi}{4} & \frac{4 \pi}{3} & \frac{3 \pi}{2} & \frac{5 \pi}{3} & \frac{7 \pi}{4} & \frac{11 \pi}{6} & 2 \pi \\
\hline \sin & 0 & -\frac{1}{2} & -\frac{\sqrt{2}}{2} & -\frac{\sqrt{3}}{2} & -1 & -\frac{\sqrt{3}}{2} & -\frac{\sqrt{2}}{2} & -\frac{1}{2} & 0 \\
\hline \cos & -1 & -\frac{\sqrt{3}}{2} & -\frac{\sqrt{2}}{2} & -\frac{1}{2} & 0 & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & 1 \\
\hline
\end{array}
$$
Proprietăţile functiilor tg şi ctg
$\operatorname{tg}(t+k \pi)=\operatorname{tg} t, \quad (\forall) t \in \mathbb{R} \backslash\left \{\left.(2 k+1) \frac{\pi}{2} \right\rvert\, k \in \mathbb{Z}\right \}$
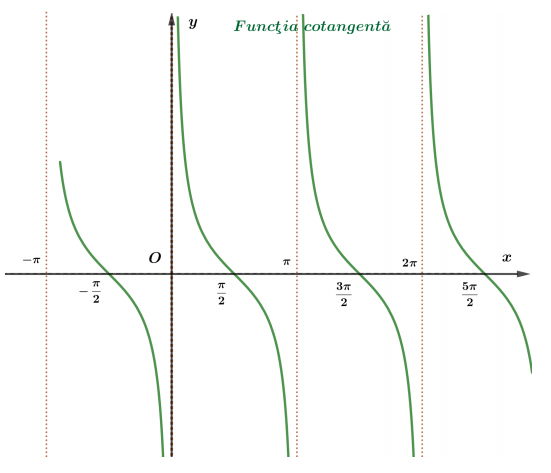
$\operatorname{ctg}(t+k \pi)=\operatorname{ctg} t , \quad (\forall) t \in \mathbb{R} \backslash{k \pi \mid k \in \mathbb{Z}}$
$\operatorname{tg}: \mathbb{R} \backslash\left \{\left.(2 k+1) \frac{\pi}{2} \right\rvert\, k \in \mathbb{Z}\right \} \rightarrow \mathbb{R}$ este o funcţie impară: $\operatorname{tg}(-t)=-\operatorname{tg} t$
$\operatorname{ctg}: \mathbb{R} \backslash{k \pi \mid k \in \mathbb{Z}} \rightarrow \mathbb{R}$ este o funcţie impară: $\operatorname{ctg}(-t)=-\operatorname{ctg} t$.
Funcţiile tg şi ctg sunt pozitive în $I$ şi $I I I$ resp. negative în $I I$ şi IV.
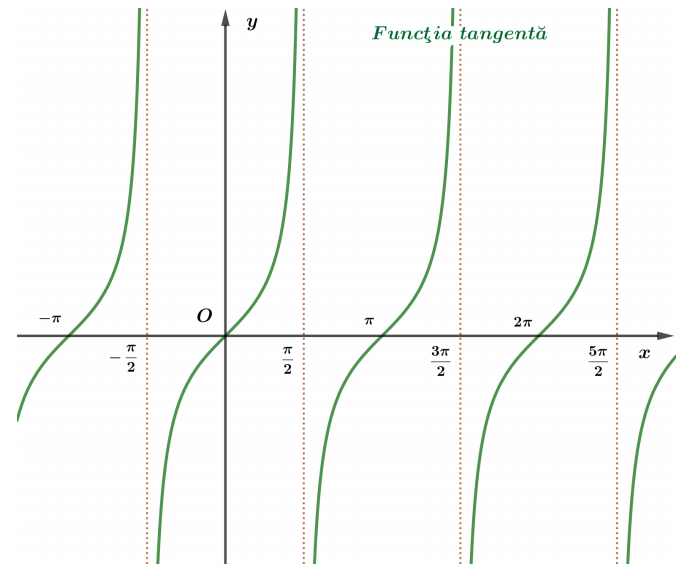
Dreptele $x=(2 k+1) \frac{\pi}{2}(k \in \mathbb{Z})$ sunt asimptote verticale la graficul funcţiei tangentă.
$$
\lim\limits_ {\substack{t \rightarrow \large\frac{\pi}{2} \\ t<\large\frac{\pi}{2}}} \operatorname{tg} t=+\infty, \quad \lim\limits_ {\substack{t \rightarrow \large\frac{\pi}{2} \\ t>\large\frac{\pi}{2}}} \operatorname{tg} t=-\infty .
$$
Dreptele $x=k \pi(k \in \mathbb{Z})$ sunt asimptote verticale la graficul funcţiei cotangentă.
$$
\lim\limits_ {\substack{t \rightarrow 0 \\ t>0}} \operatorname{ctg} t=+\infty, \quad \lim\limits_ {\substack{t \rightarrow \pi \\ t<\pi}} \operatorname{ctg} t=-\infty .
$$
$$
\begin{aligned}
&\text { Tabelul de valori al funcţiilor tg şi ctg }\\
&\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline 0 & 0 & 30 & 45 & 60 & 90 & 120 & 135 & 150 & 180 \\
\hline \operatorname{rad} & 0 & \frac{\pi}{6} & \frac{\pi}{4} & \frac{\pi}{3} & \frac{\pi}{2} & \frac{2 \pi}{3} & \frac{3 \pi}{4} & \frac{5 \pi}{6} & \pi \\
\hline \operatorname{tg} & 0 & \frac{1}{\sqrt{3}} & 1 & \sqrt{3} & \left.{ }^{+\infty}\right|_{-\infty} & -\sqrt{3} & -1 & -\frac{1}{\sqrt{3}} & 0 \\
\hline \operatorname{ctg} & -\left.\infty\right|^{+\infty} & \sqrt{3} & 1 & \frac{1}{\sqrt{3}} & 0 & -\frac{1}{\sqrt{3}} & -1 & -\sqrt{3} & -\left.\infty\right|^{+\infty} \\
\hline
\end{array}
\end{aligned}
$$
Relaţii între funcţiile trigonometrice
Formule fundamentale
$$
\sin ^2 t+\cos ^2 t=1 ; 1+\operatorname{tg}^2 t=\frac{1}{\cos ^2 t} ; 1+\operatorname{ctg}^2 t=\frac{1}{\sin ^2 t}
$$
Functiile trigonometrice ale complementului
$$
\begin{aligned}
& \sin \left(\frac{\pi}{2}-t\right)=\cos t ; \operatorname{tg}\left(\frac{\pi}{2}-t\right)=\operatorname{ctg} t \
& \cos \left(\frac{\pi}{2}-t\right)=\sin t ; \operatorname{ctg}\left(\frac{\pi}{2}-t\right)=\operatorname{tg} t
\end{aligned}
$$
Funcţiile trigonometrice ale sumei şi diferenţei de arce
$$
\begin{array}{ll}
\sin (a+b)=\sin a \cos b+\cos a \sin b ; & \sin (a-b)=\sin a \cos b-\cos a \sin b ; \\
\cos (a+b)=\cos a \cos b-\sin a \sin b ; & \cos (a-b)=\cos a \cos b+\sin a \sin b ; \\
\operatorname{tg}(a+b)=\large\frac{\operatorname{tg} a+\operatorname{tg} b}{1-\operatorname{tg} a \operatorname{tg} b} ; & \operatorname{tg}(a-b)=\large\frac{\operatorname{tg} a-\operatorname{tg} b}{1+\operatorname{tg} a \operatorname{tg} b}
\end{array}
$$
Funcţiile trigonometrice ale dublului şi triplului unui arc
$$
\begin{array}{ll}
\sin 2 t=2 \cos t \sin t ; & \sin 3 t=3 \sin t-4 \sin ^3 t ; \
\cos 2 t=2 \cos ^2 t-1=1-2 \sin ^2 t=\cos ^2 t-\sin ^2 t ; & \cos 3 t=4 \cos ^3 t-3 \cos t ; \
\operatorname{tg} 2 t=\frac{2 \operatorname{tg} t}{1-\operatorname{tg}^2 t} ; & \operatorname{tg} 3 t=\frac{3 \operatorname{tg} t-\operatorname{tg}^3 t}{1-3 \operatorname{tg}^2 t} .
\end{array}
$$
Exprimarea funcţiilor trigonometrice cu ajutorul arcului dublu
$$
\begin{aligned}
& \sin t= \pm \sqrt{\frac{1-\cos 2 t}{2}} ; \quad \cos t= \pm \sqrt{\frac{1+\cos 2 t}{2}} ; \quad \operatorname{tg} t= \pm \sqrt{\frac{1-\cos 2 t}{1+\cos 2 t}} ; \\
& \text { Semnul din faţa radicalului }\left\langle\begin{array}{l}
\text { se stabileşte cadranul ce îl conţine pe } t ; \\
\text { se alege semnul funcţiei din cadranul lui } t
\end{array}\right.
\end{aligned}
$$
Exprimarea raţională a funcţiilor trigonometrice
$$
\sin t=\frac{2 \operatorname{tg} \frac{t}{2}}{1+\operatorname{tg}^2 \frac{t}{2}} ; \quad \cos t=\frac{1-\operatorname{tg}^2 \frac{t}{2}}{1+\operatorname{tg}^2 \frac{t}{2}} ; \quad \operatorname{tg} t=\frac{2 \operatorname{tg} \frac{t}{2}}{1-\operatorname{tg}^2 \frac{t}{2}} .
$$
Transformarea sumei/diferenţei în produs
$$
\begin{array}{ll}
\sin p+\sin q=2 \sin \large \frac{p+q}{2} \cos \large \frac{p-q}{2} ; & \sin p-\sin q=2 \sin \large \frac{p-q}{2} \cos \large \frac{p+q}{2} ; \\
\cos p+\cos q=2 \cos \large \frac{p+q}{2} \cos \large \frac{p-q}{2} ; & \cos p-\cos q=-2 \sin \large \frac{p+q}{2} \sin \large \frac{p-q}{2} ; \\
\operatorname{tg} p+\operatorname{tg} q=\large \frac{\sin (p+q)}{\cos p \cos q} ; & \operatorname{tg} p-\operatorname{tg} q=\large \frac{\sin (p-q)}{\cos p \cos q} .
\end{array}
$$
Transformarea produsului în sumă/diferenţă
$$
\begin{aligned}
& \sin a \sin b= \frac{1}{2} \cos (a-b)- \frac{1}{2} \cos (a+b) ; \\
& \cos a \cos b= \frac{1}{2} \cos (a-b)+ \frac{1}{2} \cos (a+b) ; \\
& \sin a \cos b= \frac{1}{2} \sin (a+b)+ \frac{1}{2} \sin (a-b) .
\end{aligned}
$$
Funcţiile trigonometrice inverse
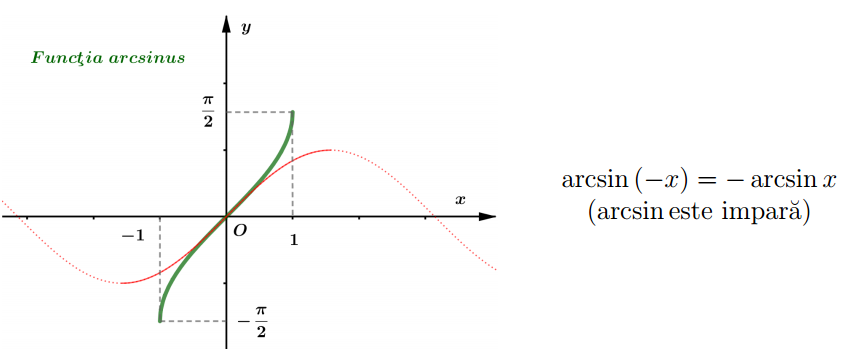
Restricţia $\sin :\left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \rightarrow[-1,1]$ este bijectivă (deci inversabilă).
Definiţie
$\arcsin a=$ “arcul cuprins intre $-\frac{\pi}{2}$ şi $\frac{\pi}{2}$ al cărui sinus este $a$ ” $\quad(-1 \leq a \leq 1)$
$$
\begin{array}{|lll|}
\hline \arcsin :[-1,1] \rightarrow\left[-\frac{\pi}{2}, \frac{\pi}{2}\right], & \begin{array}{l}
\arcsin x=y \Leftrightarrow x=\sin y \\
x \in[-1,1], \quad y \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]
\end{array}\\
\hline
\end{array}
$$
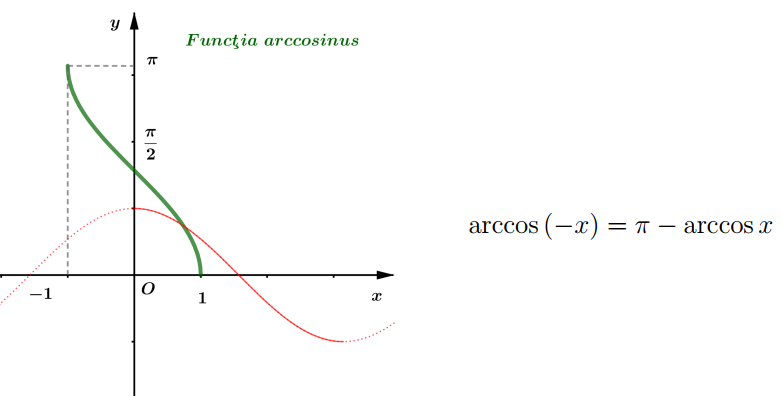
Restricţia cos : $[0, \pi] \rightarrow[-1,1]$ este bijectivă (deci inversabilă).
Definiţie $\arccos a=$ “arcul cuprins între 0 şi $\pi$ al cărui cosinus este $a$ ” $\quad(-1 \leq a \leq 1)$
$$
\begin{array}{|lll|}
\hline \arccos :[-1,1] \rightarrow\left[0, \pi \right], & \begin{array}{l}
\arccos x=y \Leftrightarrow x=\cos y \\
x \in[-1,1], \quad y \in\left[0, \pi\right]
\end{array}\\
\hline
\end{array}
$$
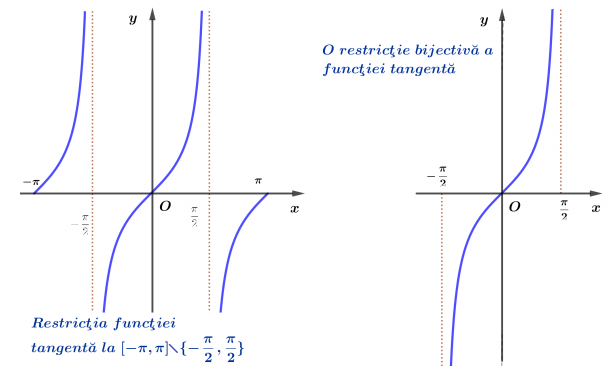
Restricţia tg : $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \rightarrow \mathbb{R}$ este bijectivă (deci inversabilă).
Definitie
$\operatorname{arctg} a=$ “arcul cuprins între $-\frac{\pi}{2}$ şi $\frac{\pi}{2}$ a cărui tangentă este $a$ ” $(a \in \mathbb{R})$
$$
\begin{array}{|lll|}
\hline \operatorname{arctg} :\mathbb{R} \rightarrow\left(-\frac{\pi}{2}, \frac{\pi}{2}\right), & \begin{array}{l}
\operatorname{arctg} x=y \Leftrightarrow x=\operatorname{tg} y \\
x \in \mathbb{R}, \quad y \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)
\end{array}\\
\hline
\end{array}
$$
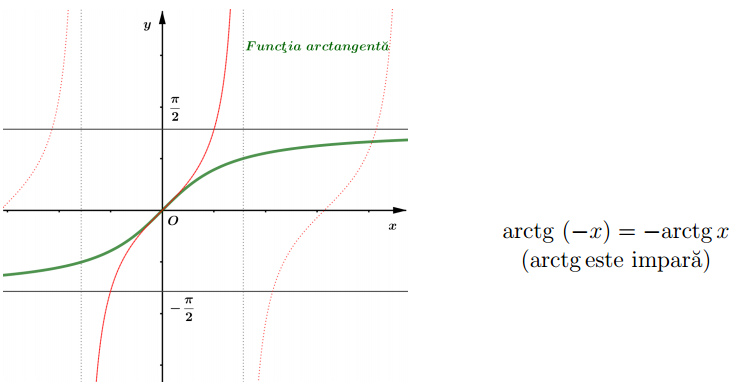
Dreptele $y=-\frac{\pi}{2}$ şi $y=\frac{\pi}{2}$ sunt asimptote orizontale la graficul funcţiei arctangentă.
$$
\lim {x \rightarrow-\infty} \operatorname{arctg} x=-\frac{\pi}{2} \text { şi } \lim {x \rightarrow \infty} \operatorname{arctg} x=\frac{\pi}{2}
$$
Relaţii remarcabile intre funçiile trigonometrice inverse
$$
\begin{gathered}
\sin (\arccos x)=\cos (\arcsin x)=\sqrt{1-x^2} \\
\arcsin x+\arccos x=\frac{\pi}{2} \\
\operatorname{arctg} x+\operatorname{arctg} \frac{1}{x}=\operatorname{sgn}(x) \cdot \frac{\pi}{2} \quad(x \in[-1,1]) \\
\operatorname{arctg} x+\operatorname{arctg} y \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \Rightarrow \operatorname{arctg} x+\operatorname{arctg} y=\operatorname{arctg} \frac{x+y}{1-x y}
\end{gathered}
$$
Ecuaţiile trigonometrice elementare
- Ecuaţia $\sin x=a$ are soluţie d.d. $a \in[-1,1]$.
Mulţimea soluţiilor sale este $\left \{(-1)^k \arcsin a+k \pi \mid k \in \mathbb{Z}\right \}$. În particular, $\sin x=0 \Leftrightarrow x \in{k \pi \mid k \in \mathbb{Z}}$. - Ecuaţia $\cos x=a$ are soluţie d.d. $a \in[-1,1]$.
Mulţimea soluţiilor sale este ${ \pm \arccos a+2 k \pi \mid k \in \mathbb{Z}}$. In particular, $\cos x=0 \Leftrightarrow x \in\left \{\left.(2 k+1) \frac{\pi}{2} \right\rvert\, k \in \mathbb{Z}\right \}$. - Ecuaţia $\operatorname{tg} x=a$ are soluţie $(\forall) a \in \mathbb{R}$.
Mulţimea soluţiilor sale este ${\operatorname{arctg} a+k \pi \mid k \in \mathbb{Z}}$.
În particular, $\operatorname{tg} x=0 \Leftrightarrow x \in{k \pi \mid k \in \mathbb{Z}}$.
Ecuaţia liniară
$$
a \cos t+b \sin t=c \quad\left(a, b, c \in \mathbb{R}, a^2+b^2>0\right)
$$
are soluţii dacă şi numai dacă $a^2+b^2 \geq c^2$.
Metode de rezolvare a ecuatiei liniare
- Substituţia $\left \{\begin{array}{l}x=\cos t \\ y=\sin t\end{array}\right.$ conduce la sistemul $\left \{\begin{array}{l}a x+b y=c \\ x^2+y^2=1\end{array}\right.$
- Substituţia $z=\operatorname{tg} \frac{t}{2}$ conduce la ecuaţia de gradul al doilea
$$
a\left(1-z^2\right)+2 b z=c\left(1+z^2\right)
$$
Această metodă are neajunsul de a pierde (eventual) soluţiile de forma $(2 k+1) \pi$.
- Metoda unghiului auxiliar constă în transformarea expresiei din membrul stâng al ecuaţiei.
$$
a \cos t+b \sin t=c \Leftrightarrow \cos t+\frac{b}{a} \sin t=\frac{c}{a} \Leftrightarrow \cos t+\operatorname{tg} \varphi \sin t=\frac{c}{a},
$$
unde $\varphi \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$, numit unghi auxiliar este unicul cu proprietatea tg $\varphi=\frac{b}{a}$. Rezultă imediat
$$
\begin{aligned}
\cos (t-\varphi) & =\frac{c}{a} \cos \varphi \Leftrightarrow \\
t & \in\left \{\left.\varphi \pm \arccos \left(\frac{c}{a} \cos \varphi\right)+2 k \pi \right\rvert\, k \in \mathbb{Z}\right \} .
\end{aligned}
$$
Aplicaţiile trigonometriei în geometrie
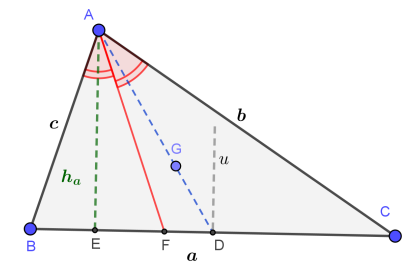
$A E \perp B C, h_a-$ lungimea înălţimii $\widehat{B A F} \equiv \widehat{C A F}, A F-$ bisectoare $B D \equiv D C, A D-$ mediană
$G$, centrul de greutate $A G=\frac{2}{3} A D$ ş $i G D=\frac{1}{3} A D$
$|D u \perp B C| D$,$u – mediatoare$
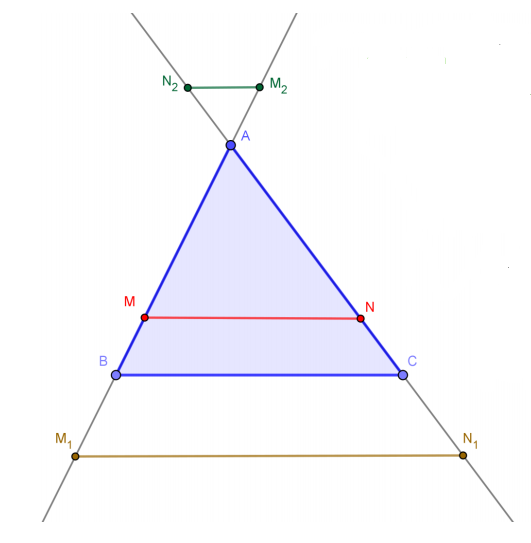
Teorema lui Thales
$$
\begin{gathered}
M_2 N_2 | B C \Rightarrow \frac{A M_2}{B M_2}=\frac{A N_2}{C N_2} \\
M N | B C \Rightarrow \frac{A M}{B M}=\frac{A N}{C N} \\
M_1 N_1 | B C \Rightarrow \frac{A M_1}{B M_1}=\frac{A N_1}{C N_1}
\end{gathered}
$$
Teorema asemănării
$$
\begin{aligned}
M N | B C \Rightarrow & \Delta A M N \sim \Delta A B C \\
& \frac{A M}{A B}=\frac{A N}{A C}=\frac{M N}{B C}(=\rho)
\end{aligned}
$$
$\rho$, raportul de asemănare $\frac{S_{A M N}}{S_{A B C}}=\rho^2$
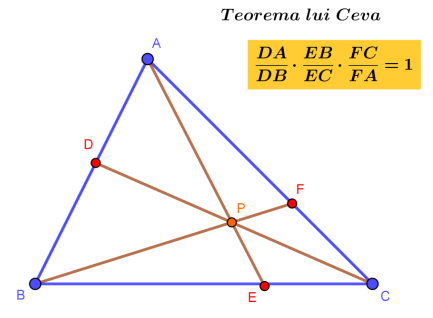
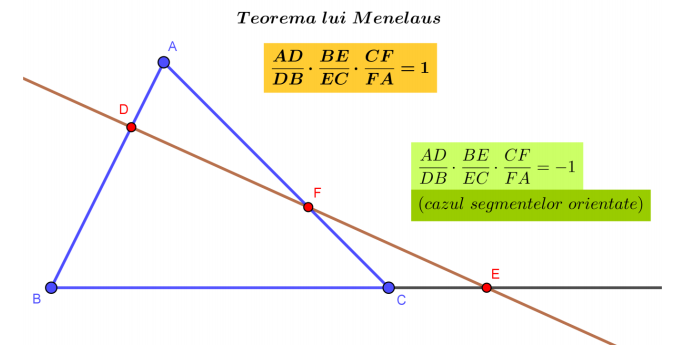
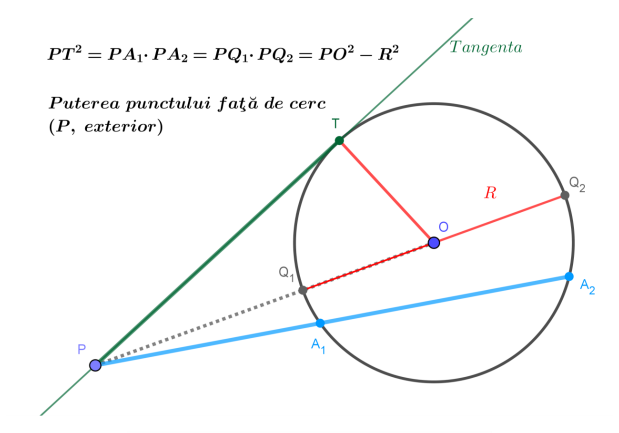
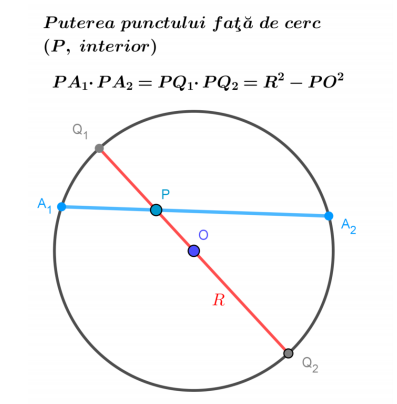
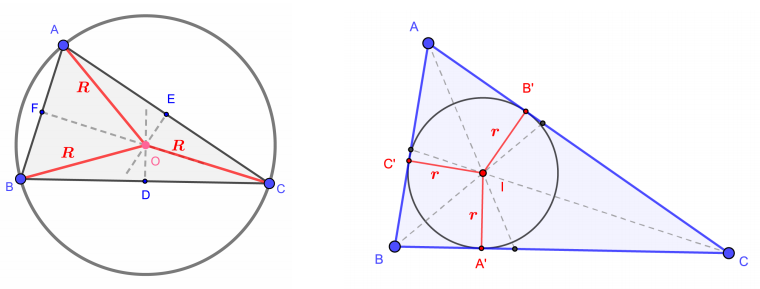
Teorema sinusurilor
$$
\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2 R
$$
Teorema cosinusului
$$
\begin{aligned}
& a^2=b^2+c^2-2 b c \cos A \\
& b^2=c^2+a^2-2 c a \cos B \\
& c^2=a^2+b^2-2 a b \cos C
\end{aligned}
$$
Aria triunghiului
$$
\begin{aligned}
& S=\frac{a h_a}{2} \quad=\frac{b h_b}{2} \quad=\frac{c h_c}{2} \\
& S=\frac{b c \sin A}{2} \quad=\frac{c a \sin B}{2} \quad=\frac{a b \sin C}{2} \\
& S=\frac{a^2 \sin B \sin C}{2 \sin A}=\frac{b^2 \sin C \sin A}{2 \sin B}=\frac{c^2 \sin A \sin B}{2 \sin C} \\
& \qquad \begin{aligned}
S & =2 R^2 \sin A \sin B \sin C \\
S & =r^2 \operatorname{ctg} \frac{A}{2} \operatorname{ctg} \frac{B}{2} \operatorname{ctg} \frac{C}{2} \\
S & =p r \\
S & =\frac{a b c}{4 R}
\end{aligned} \\
& S=\sqrt{p(p-a)(p-b)(p-c)} \quad \text { (formula lui Heron) }
\end{aligned}
$$
Numere complexe
Aplicaţiile trigonometriei în algebră
$$\mathbb{C}=\left \{z=x+i y \mid x, y \in \mathbb{R}, i^2=-1\right \} \text {-mulţimea numerelor complexe }$$
$$
\begin{array}{ll}
z=x+i y & , \text { forma algebrică a numărului complex } z \\
\operatorname{Re} z=x & , \text { partea reală a numărului complex } z \\
\operatorname{Im} z=y & , \text { partea imaginară a numărului complex } z \\
|z|=\sqrt{x^2+y^2} & , \text { modulul numărului complex } z \\
\bar{z}=x-i y & , \text { conjugatul numărului complex } z \\
z \cdot \bar{z}=|z|^2 &
\end{array}
$$
Numărul complex $z=x+i y$ este afixul punctului $M(x, y)$ iar conjugatul său, $\bar{z}=x-i y$, este afixul simetricului punctului $M(x, y)$ faţă de axa $O x$.
- se notează prin $t$ unghiul format de dreapta $O M(M \neq O)$ cu semiaxa pozitivă $O x$ (argumentul lui $z$ );
- se notează prin $r$ lungimea segmentului $O M($ modulul lui $z)$;
- din definiţia funcţiilor trigonometrice rezultă
$$
\begin{gathered}
\left \{\begin{array}{l}
x=r \cos t \\
y=r \sin t
\end{array} \quad(r>0 \text { iar } t \in[0,2 \pi)) .\right. \\
z=r(\cos t+i \sin t) \text { forma trigonometrică a lui } z
\end{gathered}
$$
Numerele $r$ şi $t$ sunt cordonatele polare ale punctului $M(x, y): r$ este raza polară, $O$ este polul iar $t$ este argumentul lui $z$.
$$
\begin{gathered}
r=\sqrt{x^2+y^2} \\
t=\operatorname{arctg} \frac{y}{x}+k \pi \\
(k=0 \text { pt. } M \in C a d r I, \quad k=1 \text { pt. } M \in C a d r I I-I I I, \quad k=2 \text { pt. } M \in C a d r I V) .
\end{gathered}
$$
Înmulţirea şi împărţirea numerelor complexe $z_j=r_j\left(\cos t_j+i \sin t_j\right), \quad j=\overline{1,2}$
$$
\begin{aligned}
& z_1 z_2=r_1 r_2\left[\cos \left(t_1+t_2\right)+i \sin \left(t_1+t_2\right)\right] \\
& \frac{z_1}{z_2}=\frac{r_1}{r_2}\left[\cos \left(t_1-t_2\right)+i \sin \left(t_1-t_2\right)\right]
\end{aligned}
$$
Formula lui Moivre
$$
z=r(\cos t+i \sin t) \Rightarrow z^n=r^n[\cos n t+i \sin n t]
$$
Rădăcina complexă de ordinul $n$ a numărului complex $z=r(\cos t+i \sin t)$ :
$$
\sqrt[n]{z}=\sqrt[n]{r}\left(\cos \frac{t+2 k \pi}{n}+i \sin \frac{t+2 k \pi}{n}\right), \quad k=\overline{0, n-1}
$$
Elemente de geometrie analitică
Vectori
Versorii axelor de coordonate: $\overline{\mathbf{i}}=(1,0)$ şi $\overline{\mathbf{j}}=(0,1)$.
Vectorul de poziţie al punctului $M(x, y): \overline{O M}=x \overline{\mathbf{i}}+y \overline{\mathbf{j}}$.
Lungimea vectorului $\overline{O M}$ (distanţa dintre M şi origine):
$$
\begin{aligned}
|O M|^2 & =x^2+y^2 \
O M^2 & =x^2+y^2 .
\end{aligned}
$$
Vectorul cu originea $T(a, b)$ şi extremitatea $M(x, y)$ :
$$
\overline{T M}=(x-a) \overline{\mathbf{i}}+(y-b) \overline{\mathbf{j}} .
$$
Lungimea vectorului $\overline{T M}$ (distanţa dintre punctele $T(a, b)$ şi $M(x, y)$ ):
$$
|\overline{T M}|=T M=\sqrt{(x-a)^2+(y-b)^2} .
$$
İmpărţirea segmentului $P Q$ în raportul $k \in \mathbb{R} \backslash{-1}: \overline{P M}=k \overline{M Q}$
$$
P\left(x_1, y_1\right), Q\left(x_2, y_2\right) \Rightarrow M(x, y) \quad \text { cu } \quad x=\frac{x_1+k x_2}{1+k} \text { şi } y=\frac{y_1+k y_2}{1+k} .
$$
Caz particular $k=1$, mijlocul segmentului $P Q: M\left(\large\frac{x_1+x_2}{2}, \large\frac{y_1+y_2}{2}\right)$.
Dreapta în plan
- Ecuația generală explicită : $y=m x+n$
( $m$, panta dreptei : $m=\operatorname{tg} \varphi$, unde $\varphi$ este unghiul dintre dreaptă şi semiaxa pozitivă $O x$ ).
(Dreptele paralele cu axa $O y$ – dreptele verticale – sunt caracterizate prin ecuaţia $x=p$; panta acestora este infinită.) - Ecuaţia generală implicită : $A x+B y+C=0 \quad\left(m=-\frac{A}{B}\right)$.
- Ecuaţia dreptei prin tăieturi : $\frac{x}{a}+\frac{y}{b}=1$ (dreapta taie $O x$ în $a$ şi $O y$ în $b$ ).
- Ecuaţia dreptei ce trece prin $T(a, b)$ şi are panta $m: y-b=m(x-a)$.
- Ecuaţia dreptei ce trece prin $T(a, b)$ şi $S(u, v):\left|\begin{array}{lll}x & y & 1 \\ a & b & 1 \\ u & v & 1\end{array}\right|=0$.
Aria triunghiului $A B C$ cu $A\left(a_1, a_2\right), B\left(b_1, b_2\right), C\left(c_1, c_2\right)$ :
$$
\mathcal{A}=\frac{1}{2} \bmod \left|\begin{array}{lll}
a_1 & a_2 & 1 \\
b_1 & b_2 & 1 \\
c_1 & c_2 & 1
\end{array}\right| \quad \text { (adică modulul determinantului) }
$$
$A, B, C$ sunt coliniare $\Leftrightarrow \mathcal{A}=0$.
Distanţa de la punctul $T(a, b)$ la dreapta (d) $A x+B y+C=0$
$$
\operatorname{dist}(d, T)=\frac{|A a+B b+C|}{\sqrt{A^2+B^2}}
$$
În cazul dreptelor exprimate explicit (de pantă finită)
$$
\left(d_1\right) |\left(d_2\right) \Leftrightarrow m_1=m_2
$$
$\left(d_1\right) \perp\left(d_2\right) \Leftrightarrow m_1 \cdot m_2=-1$ (relaţie utilă la determinarea normalei!).
Cercul
Cercul este locul geometric al punctelor egal depărtate de un punct fix (numit centru).
- Ecuaţia cercului de rază $r$ şi centru $C(u, v)$
$$
(x-u)^2+(y-v)^2=r^2 .
$$
- Ecuaţia generală a cercului : $x^2+y^2+a \cdot x+b \cdot y+c=0$.
- Ecuaţia cercului ce trece prin punctele $A(m, n), B(s, t)$ şi $C(p, q)$
$$
\left|\begin{array}{cccc}
x^2+y^2 & x & y & 1 \\
m^2+n^2 & m & n & 1 \\
s^2+t^2 & s & t & 1 \\
p^2+q^2 & p & q & 1
\end{array}\right|=0
$$
$$
\text { Intersecţia dreptei cu cercul }=\text { soluţia sistemului: }\left \{\begin{array}{c}
x^2+y^2+a \cdot x+b \cdot y+c=0 \\
y=m x+n
\end{array}\right. \text {. }
$$

